题目内容
8.函数f(x)=$\left\{\begin{array}{l}{{e}^{x+1}(x<0)}\\{\sqrt{-{x}^{2}+2x}(0≤x≤2)}\end{array}\right.$,若函数g(x)=f(x)-kx-2k恰有两个零点,则实数k的取值范围是[0,$\frac{\sqrt{2}}{4}$)∪(1,$\frac{e}{2}$).分析 由题意可得,f(x)=k(x+2)有两个不等的实根,作出y=f(x)的图象和直线y=k(x+2),通过图象观察它们有两个交点的情况,注意运用导数求切线的斜率和直线和圆相切的条件:d=r.
解答 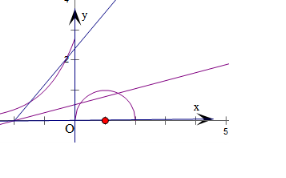 解:函数g(x)=f(x)-kx-2k恰有两个零点,
解:函数g(x)=f(x)-kx-2k恰有两个零点,
即为f(x)=k(x+2)有两个不等的实根,
作出y=f(x)的图象和直线y=k(x+2),
当x<0时,直线和曲线相切,设切点为(m,km+2k),
由em+1=km+2k=k,k≠0,解得k=1,m=-1,
当直线经过点(0,e),k=$\frac{e}{2}$,
由图象可知,当1<k<$\frac{e}{2}$时,直线和曲线有两个交点,
当直线和半圆相切,d=r=1,圆心为(1,0),
由$\frac{|3k|}{\sqrt{1+{k}^{2}}}$=1,解得k=$\frac{\sqrt{2}}{4}$(负的舍去),
由图象可得,0≤k<$\frac{\sqrt{2}}{4}$时,直线和半圆有两个交点.
则有k的取值范围是[0,$\frac{\sqrt{2}}{4}$)∪(1,$\frac{e}{2}$).
故答案为:[0,$\frac{\sqrt{2}}{4}$)∪(1,$\frac{e}{2}$).
点评 本题考查函数的零点的求法,主要考查函数和方程的转化思想,运用数形结合的思想方法是解题的关键.

练习册系列答案
相关题目
16.已知命题p:“数列{an}满足an+2=3an+1-2an(n≥2)”,命题q:“数列{an+1-an}是公比为2的等比数列”,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.某学科测试中要求考生从A,B,C三道题中任选一题作答,考试结束后,统计数据显示共有600名学生参加测试,选择A,B,C三题答卷数如表:
(Ⅰ)某教师为了解参加测试的学生答卷情况,现用分层抽样的方法从600份答案中抽出若干份答卷,其中从选择A题作答的答卷中抽出了3份,则应分别从选择B,C题作答的答卷中各抽出多少份?
(Ⅱ)若在(Ⅰ)问中被抽出的答卷中,A,B,C三题答卷得优的份数都是2,从被抽出的A,B,C三题答卷中再各抽出1份,求这3份答卷中恰有1份得优的概率;
(Ⅲ)测试后的统计数据显示,B题的答卷得优的有100份,若以频率作为概率,在(Ⅰ)问中被抽出的选择B题作答的答卷中,记其中得优的份数为X,求X的分布列及其数学期望EX.
| 题 | A | B | C |
| 答卷数 | 180 | 300 | 120 |
(Ⅱ)若在(Ⅰ)问中被抽出的答卷中,A,B,C三题答卷得优的份数都是2,从被抽出的A,B,C三题答卷中再各抽出1份,求这3份答卷中恰有1份得优的概率;
(Ⅲ)测试后的统计数据显示,B题的答卷得优的有100份,若以频率作为概率,在(Ⅰ)问中被抽出的选择B题作答的答卷中,记其中得优的份数为X,求X的分布列及其数学期望EX.
