题目内容
14.已知函数f(x)=lnx-ax+1,x∈(0,+∞),a∈R)(1)谈论函数f(x)在定义域内的极值点的个数
(2)设g(x)=mx-1(m>0),在a=1时,求方程f(x)-g(x)=0的解的个数
(3)求证:(1+$\frac{3}{2×4}$)(1+$\frac{9}{4×10}$)(1+$\frac{27}{10×28}$)…[1+$\frac{{3}^{n}}{{{(3}^{n-1}+1)(3}^{n}+1)}$<${e}^{\frac{3}{4}}$,(其中n∈N*,e是自然对数的底)
分析 (1)求出导数,对a讨论,当a≤0时,当a>0时,判断函数的单调性,即可得到极值点的个数;
(2)令h(x)=lnx+2-(m+1)x,h′(x)=$\frac{1}{x}$-(m+1),求得最大值,讨论最大值为0,小于0,大于0,即可得到零点的个数;
(3)首先证明ln(x+1)≤x在[0,+∞)上恒成立,利用裂项法,结合对数的运算法则,可证结论
解答 解:(1)函数f(x)=lnx-ax+1的导数为f′(x)=$\frac{1}{x}$-a,
当a≤0时,f′(x)>0恒成立,f(x)在(0,+∞)递增,无极值点;
当a>0时,x>$\frac{1}{a}$时,f′(x)<0,f(x)递减,当0<x<$\frac{1}{a}$时,f′(x)>0,f(x)递增.
f(x)在x=$\frac{1}{a}$处取得极大值,无极小值,则极值点为1个,
综上可得a>0,f(x)有一个极值点;a≤0时,f(x)无极值点.
(2)方程f(x)-g(x)=0,即为lnx+2-(m+1)x=0,
令h(x)=lnx+2-(m+1)x,h′(x)=$\frac{1}{x}$-(m+1),
由m>0,则可得x=$\frac{1}{m+1}$处导数左正右负,
h(x)取得极大值,也为最大值,且为1-ln(m+1),
若1-ln(1+m)<0,即有m>e-1,方程f(x)-g(x)=0的解的个数为0;
若1-ln(1+m)=0,即有m=e-1,方程f(x)-g(x)=0的解的个数为1;
若1-ln(1+m)>0,即有0<m<e-1,方程f(x)-g(x)=0的解的个数为2.
(3)证明:令m(x)=ln(x+1)-x,x>0,
m′(x)=$\frac{1}{1+x}$-1=$\frac{-x}{1+x}$,当x>0时,m′(x)<0,m(x)递减,
即有m(x)≤m(0)=0,
即ln(1+x)≤x.
令x=$\frac{{3}^{n}}{({3}^{n-1}+1)({3}^{n}+1)}$,则ln(1+$\frac{{3}^{n}}{({3}^{n-1}+1)({3}^{n}+1)}$)<$\frac{{3}^{n}}{({3}^{n-1}+1)({3}^{n}+1)}$=$\frac{3}{2}$($\frac{1}{{3}^{n-1}+1}$-$\frac{1}{{3}^{n}+1}$),
即有ln(1+$\frac{3}{2×4}$)+ln(1+$\frac{9}{4×10}$)+ln(1+$\frac{27}{10×28}$)+…+ln[1+$\frac{{3}^{n}}{{{(3}^{n-1}+1)(3}^{n}+1)}$
<$\frac{3}{2}$($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{10}$+$\frac{1}{10}$-$\frac{1}{28}$+…+$\frac{1}{{3}^{n-1}+1}$-$\frac{1}{{3}^{n}+1}$)=$\frac{3}{2}$(-$\frac{1}{{3}^{n}+1}$)<$\frac{3}{4}$.
则有(1+$\frac{3}{2×4}$)(1+$\frac{9}{4×10}$)(1+$\frac{27}{10×28}$)•…•[1+$\frac{{3}^{n}}{{{(3}^{n-1}+1)(3}^{n}+1)}$<${e}^{\frac{3}{4}}$成立.
点评 本题考查导数知识的运用,考查函数的单调性和极值点个数及零点个数,考查不等式的证明,考查分类讨论的数学思想,属于难题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱BC,DD1上的点,如果B1E⊥平面ABF,则CE与DF的长度之和为( )
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱BC,DD1上的点,如果B1E⊥平面ABF,则CE与DF的长度之和为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{3}$ |

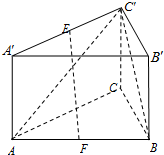 如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.
如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点. 在如图所示的几何体中,四边形ABCD是矩形,AB=2BC=4,四边形CDEF是等腰梯形,EF∥DC,EF=2,且平面ABCD⊥平面CDEF,AF⊥CF.
在如图所示的几何体中,四边形ABCD是矩形,AB=2BC=4,四边形CDEF是等腰梯形,EF∥DC,EF=2,且平面ABCD⊥平面CDEF,AF⊥CF.