题目内容
17.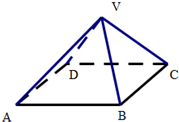 如图:正四棱锥V-ABCD中,高为2,底面ABCD是边长为4的正方形,则二面角V-AB-C的平面角为45°.
如图:正四棱锥V-ABCD中,高为2,底面ABCD是边长为4的正方形,则二面角V-AB-C的平面角为45°.
分析 根据二面角的平面角的定义先找出二面角的平面角,然后结合三角形的边角关系进行求解即可.
解答 解:连接AC,BD交于O点,取AB的中点E, 连接OE,VE,则在正四棱锥V-ABCD中,有OE⊥AB,VE⊥AB,
连接OE,VE,则在正四棱锥V-ABCD中,有OE⊥AB,VE⊥AB,
即∠VEO是二面角V-AB-C的平面角,
∵底面ABCD是边长为4的正方形,高为2,
∴OE=2,
在△VOE中,tan∠VEO=$\frac{V0}{OE}=\frac{2}{2}=1$,
即∠VEO=45°,
故答案为:45°
点评 本题主要考查二面角的求解,根据二面角平面角的定义,先找出平面角是解决本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
20.某学科测试中要求考生从A,B,C三道题中任选一题作答,考试结束后,统计数据显示共有600名学生参加测试,选择A,B,C三题答卷数如表:
(Ⅰ)某教师为了解参加测试的学生答卷情况,现用分层抽样的方法从600份答案中抽出若干份答卷,其中从选择A题作答的答卷中抽出了3份,则应分别从选择B,C题作答的答卷中各抽出多少份?
(Ⅱ)若在(Ⅰ)问中被抽出的答卷中,A,B,C三题答卷得优的份数都是2,从被抽出的A,B,C三题答卷中再各抽出1份,求这3份答卷中恰有1份得优的概率;
(Ⅲ)测试后的统计数据显示,B题的答卷得优的有100份,若以频率作为概率,在(Ⅰ)问中被抽出的选择B题作答的答卷中,记其中得优的份数为X,求X的分布列及其数学期望EX.
| 题 | A | B | C |
| 答卷数 | 180 | 300 | 120 |
(Ⅱ)若在(Ⅰ)问中被抽出的答卷中,A,B,C三题答卷得优的份数都是2,从被抽出的A,B,C三题答卷中再各抽出1份,求这3份答卷中恰有1份得优的概率;
(Ⅲ)测试后的统计数据显示,B题的答卷得优的有100份,若以频率作为概率,在(Ⅰ)问中被抽出的选择B题作答的答卷中,记其中得优的份数为X,求X的分布列及其数学期望EX.
2. 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱BC,DD1上的点,如果B1E⊥平面ABF,则CE与DF的长度之和为( )
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱BC,DD1上的点,如果B1E⊥平面ABF,则CE与DF的长度之和为( )
 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱BC,DD1上的点,如果B1E⊥平面ABF,则CE与DF的长度之和为( )
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱BC,DD1上的点,如果B1E⊥平面ABF,则CE与DF的长度之和为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{3}$ |
7.某大学的一个社会实践调查小组,在对大学生的良好“光盘习惯”的调查中,随机发放了120份问卷,对回收的100份有效问卷进行统计,得到如下2×2列联表:
(1)现已按是否做到关盘分层从45份女生问卷中抽取了9份问卷,若从这9份问卷中随机抽取4份,并记其中能做到光盘的问卷的分数为ξ,试求随机变量ξ的分布列和数学期望;
(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过P,那么,根据临界值表,最精确的P的值应为多少?请说明理由.
| 做不到光盘 | 能做到光盘 | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 合计 | 70 | 25 | 100 |
(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过P,那么,根据临界值表,最精确的P的值应为多少?请说明理由.

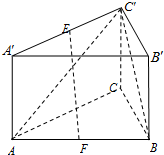 如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.
如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.