题目内容
【题目】设a,b,c分别是![]() 的三条边,且
的三条边,且![]() .我们知道,如果
.我们知道,如果![]() 为直角三角形,那么
为直角三角形,那么![]() (勾股定理).反过来,如果
(勾股定理).反过来,如果![]() ,那么
,那么![]() 为直角三角形(勾股定理的逆定理).由此可知,
为直角三角形(勾股定理的逆定理).由此可知,![]() 为直角三角形的充要条件是
为直角三角形的充要条件是![]() .请利用边长a,b,c分别给出
.请利用边长a,b,c分别给出![]() 为锐角三角形和钝角三角形的一个充要条件,并证明.
为锐角三角形和钝角三角形的一个充要条件,并证明.
【答案】![]() 为锐角三角形的充要条件是
为锐角三角形的充要条件是![]() .
.![]() 为钝角三角形的充要条件是
为钝角三角形的充要条件是![]() .证明见解析
.证明见解析
【解析】
根据勾股定理易得![]() 为锐角三角形的充要条件是
为锐角三角形的充要条件是![]() .
.![]() 为钝角三角形的充要条件是
为钝角三角形的充要条件是![]() .再分别证明充分与必要性即可.
.再分别证明充分与必要性即可.
解:(1)设a,b,c分别是![]() 的三条边,且
的三条边,且![]() ,
,![]() 为锐角三角形的充要条件是
为锐角三角形的充要条件是![]() .
.
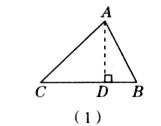
证明如下:必要性:在![]() 中,
中,![]() 是锐角,作
是锐角,作![]() ,D为垂足,如图(1).
,D为垂足,如图(1).
显然![]()
![]() ,即
,即![]() .
.
充分性:在![]() 中,
中,![]() ,
,![]() 不是直角.
不是直角.
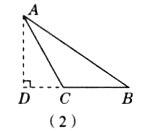
假设![]() 为钝角,如图(2).作
为钝角,如图(2).作![]() ,交BC延长线于点D.
,交BC延长线于点D.
则![]()
![]() .
.
即![]() ,与“
,与“![]() ”矛盾.
”矛盾.
故![]() 为锐角,即
为锐角,即![]() 为锐角三角形.
为锐角三角形.
(2)设a,b,c分别是![]() 的三条边,且
的三条边,且![]() ,
,![]() 为钝角三角形的充要条件是
为钝角三角形的充要条件是![]() .
.
证明如下:必要性:在![]() 中,
中,![]() 为钝角,如图(2),显然:
为钝角,如图(2),显然:
![]()
![]() .即
.即![]() .
.
充分性:在![]() 中,
中,![]() ,
,
![]() 不是直角,假设
不是直角,假设![]() 为锐角,如图(1),
为锐角,如图(1),
则![]()
![]() .即
.即![]() ,这与“
,这与“![]() ”矛盾,从而
”矛盾,从而![]() 必为钝角,即
必为钝角,即![]() 为钝角三角形.
为钝角三角形.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】随着网络的飞速发展,人们的生活发生了很大变化,其中无现金支付是一个显著特征,某评估机构对无现金支付的人群进行网络问卷调查,并从参与调查的数万名受访者中随机选取了300人,把这300人分为三类,即使用支付宝用户、使用微信用户、使用银行卡用户,各类用户的人数如图所示,同时把这300人按年龄分为青年人组与中年人组,制成如图所示的列联表:
支付宝用户 | 非支付宝用户 | 合计 | |
中老年 | 90 | ||
青年 | 120 | ||
合计 | 300 |

(1) 完成列联表,并判断是否有99%的把握认为使用支付宝用户与年龄有关系?
(2)把频率作为概率,从所有无现金支付用户中(人数很多)随机抽取3人,用![]() 表示所选3人中使用支付宝用户的人数,求
表示所选3人中使用支付宝用户的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中![]() .
.


