题目内容
【题目】某校为了增强学生的记忆力和辨识力,组织了一场类似《最强大脑》的PK赛,![]() 两队各由4名选手组成,每局两队各派一名选手PK,比赛四局.除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛A队选手获胜的概率均为
两队各由4名选手组成,每局两队各派一名选手PK,比赛四局.除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛A队选手获胜的概率均为![]() ,且各局比赛结果相互独立,比赛结束时A队的得分高于B队的得分的概率为( )
,且各局比赛结果相互独立,比赛结束时A队的得分高于B队的得分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
先确定A队的得分高于B队的得分的情况,再分类讨论利用独立事件乘法公式求对应情况的概率,最后根据加法计数原理求结果.
A队的得分高于B队的得分的情况有三种:A队的得分为5分,A队的得分为4分,A队的得分为3分.
当A队的得分为5分时,概率为![]()
当A队的得分为4分时,概率为![]()
当A队的得分为3分时,概率为![]()
因此所求概率为
![]()
故选:C

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】为抑制房价过快上涨和过度炒作,各地政府响应中央号召,因地制宜出台了系列房价调控政策.某市为拟定出台“房产限购的年龄政策”![]() 为了解人们对“房产限购年龄政策”的态度,对年龄在
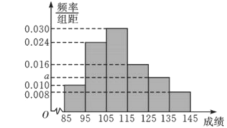
为了解人们对“房产限购年龄政策”的态度,对年龄在![]() 岁的人群中随机调查100人,调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如下:
岁的人群中随机调查100人,调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如下:
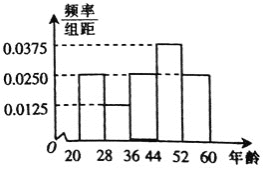
年龄 |
|
|
|
|
|
支持的人数 | 15 | 5 | 15 | 28 | 17 |
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异;
的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异;
44岁以下 | 44岁及44岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(2)若以44岁为分界点,从不支持“房产限购”的人中按分层抽样的方法抽取8人参加政策听证会.现从这8人中随机抽2人.
①抽到1人是44岁以下时,求抽到的另一人是44岁以上的概率.
②记抽到44岁以上的人数为X,求随机变量X的分布列及数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
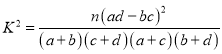 ,其中
,其中![]() .
.