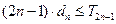题目内容
设非负等差数列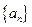 的公差
的公差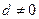 ,记
,记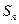 为数列
为数列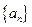 的前n项和,证明:
的前n项和,证明:
1)若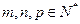 ,且
,且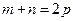 ,则
,则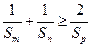 ;
;
2)若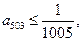 则
则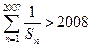 。
。
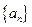 的公差
的公差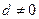 ,记
,记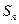 为数列
为数列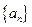 的前n项和,证明:
的前n项和,证明:1)若
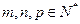 ,且
,且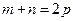 ,则
,则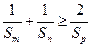 ;
;2)若
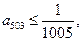 则
则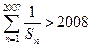 。
。证明略
设非负等差数列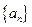 的首项为
的首项为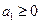 ,公差为
,公差为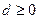 。
。
(1)因为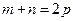 ,所以
,所以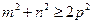 ,
,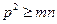 ,
,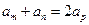 。
。
从而有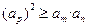 。 因为
。 因为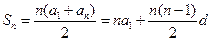 ,所以有
,所以有
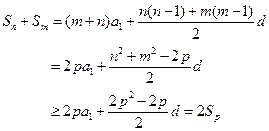

于是
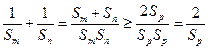 。
。
(2)
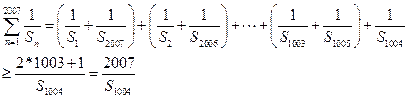
又因为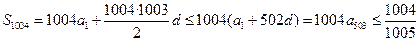 ,所以有
,所以有
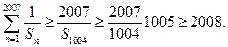
 的首项为
的首项为 ,公差为
,公差为 。
。(1)因为
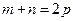 ,所以
,所以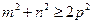 ,
,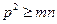 ,
,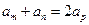 。
。从而有
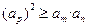 。 因为
。 因为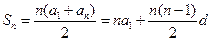 ,所以有
,所以有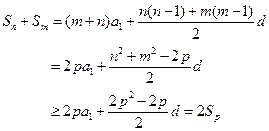

于是
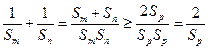 。
。(2)
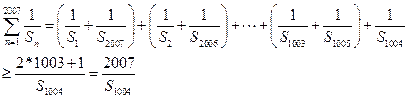
又因为
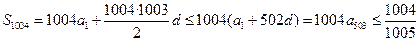 ,所以有
,所以有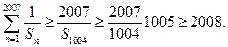

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 满足
满足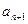 ≤
≤ . (1)若
. (1)若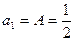 ,
,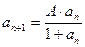 时,求
时,求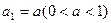 ,A=1,证明:
,A=1,证明: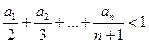
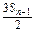 总成等差数列.
总成等差数列.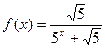 ,
,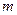 为正整数.
为正整数.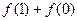 和
和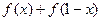 的值;
的值;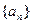 的通项公式为
的通项公式为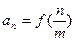 (
(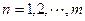 ),求数列
),求数列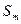 ;
;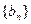 满足:
满足: ,
,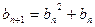 ,设
,设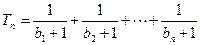 ,若(Ⅱ)中的
,若(Ⅱ)中的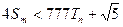 恒成立,试求m的最大值.
恒成立,试求m的最大值.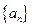 中,设
中,设 .
.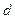 为公差的等差数列,求证
为公差的等差数列,求证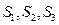 也是等差数列,并求其公差;
也是等差数列,并求其公差;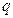 为公比的等比数列,求证
为公比的等比数列,求证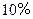 ,那么从今年起大约几年可使总销售量达到30000台(结果保留到个位)?
,那么从今年起大约几年可使总销售量达到30000台(结果保留到个位)? 是等差数列.
是等差数列.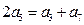 是否成立?
是否成立?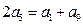 呢?为什么?
呢?为什么?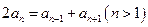 是否成立?据此你能得出什么结论?
是否成立?据此你能得出什么结论?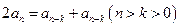 是否成立?你又能得出什么结论?
是否成立?你又能得出什么结论?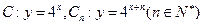 ,从
,从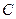 上的点
上的点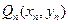 作
作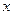 轴的垂线,交
轴的垂线,交 于点
于点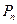 ,再从点
,再从点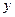 轴的垂线,交
轴的垂线,交 ,设
,设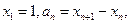

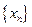 的通项公式;
的通项公式; ,数列
,数列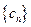 的前
的前 项和为
项和为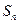 ,试比较
,试比较 的大小
的大小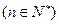 ;
;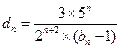 ,数列
,数列 的前
的前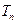 ,试证明:
,试证明: