题目内容
(本小题满分16分)
已知数列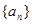 ,
,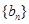 ,且满足
,且满足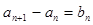 (
(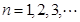 ).
).
(1)若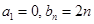 ,求数列
,求数列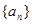 的通项公式;
的通项公式;
(2)若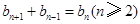 ,且
,且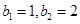 .记
.记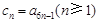 ,求证:数列
,求证:数列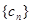 为常数列;
为常数列;
(3)若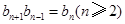 ,且
,且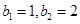 .若数列
.若数列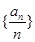 中必有某数重复出现无数次,求首项
中必有某数重复出现无数次,求首项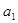 应满足的条件.
应满足的条件.
已知数列
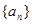 ,
,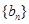 ,且满足
,且满足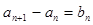 (
(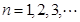 ).
).(1)若
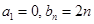 ,求数列
,求数列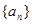 的通项公式;
的通项公式;(2)若
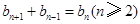 ,且
,且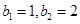 .记
.记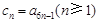 ,求证:数列
,求证:数列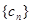 为常数列;
为常数列;(3)若
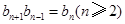 ,且
,且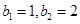 .若数列
.若数列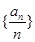 中必有某数重复出现无数次,求首项
中必有某数重复出现无数次,求首项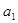 应满足的条件.
应满足的条件.(1)数列
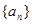 的通项为
的通项为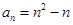 . (2)见解析;
. (2)见解析;(3)当
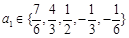 时,数列
时,数列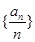 中必有某数重复出现无数次.
中必有某数重复出现无数次. 本试题主要是考查了数列的通项公式的求解,以及数列的概念和数列的单调性的运用。
(1)当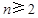 时,有累加法得到
时,有累加法得到

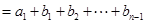
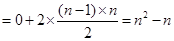 ,
,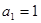 也满足上式,
也满足上式,
所以数列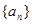 的通项为
的通项为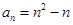 .
.
(2)因为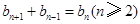 ,
,
所以对任意的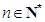 有
有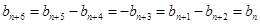 ,
,
所以数列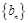 是一个以6为周期的循环数列
是一个以6为周期的循环数列
进而证明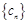 为常数列
为常数列
(3)因为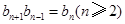 ,且
,且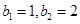 ,所以
,所以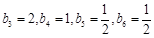 ,
,
且对任意的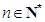 ,有
,有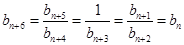 ,
,
设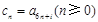 ,(其中
,(其中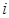 为常数且
为常数且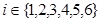 ),所以
),所以
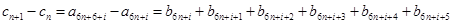
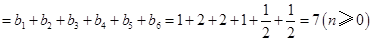 ,
,
所以数列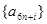 均为以7为公差的等差数列.记
均为以7为公差的等差数列.记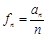 ,构造新数列来分析周期性和最值问题。
,构造新数列来分析周期性和最值问题。
(1)当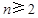 时,有
时,有
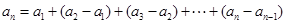
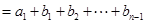 ……………………1分
……………………1分
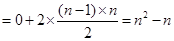 ,
,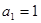 也满足上式,
也满足上式,
所以数列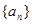 的通项为
的通项为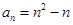 . ………………………………………………………3分
. ………………………………………………………3分
(2)因为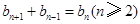 ,
,
所以对任意的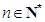 有
有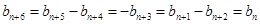 ,
,
所以数列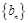 是一个以6为周期的循环数列……………………………………………………5分
是一个以6为周期的循环数列……………………………………………………5分
又因为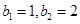 ,所以
,所以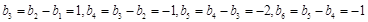
所以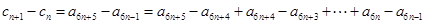

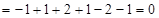
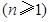 ,
,
所以数列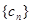 为常数列. ……………………………………………………………………7分
为常数列. ……………………………………………………………………7分
(3)因为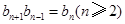 ,且
,且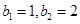 ,所以
,所以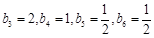 ,
,
且对任意的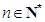 ,有
,有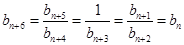 ,
,
设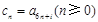 ,(其中
,(其中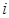 为常数且
为常数且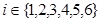 ),所以
),所以
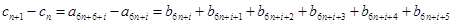
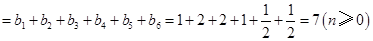 ,
,
所以数列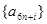 均为以7为公差的等差数列.……………………………………………10分
均为以7为公差的等差数列.……………………………………………10分
记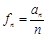 ,则
,则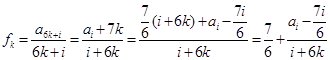 ,
,
(其中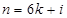
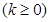 ,
,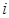 为
为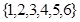 中的一个常数),
中的一个常数),
当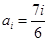 时,对任意的
时,对任意的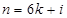 有
有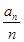
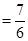 ;…………………………………………12分
;…………………………………………12分
当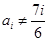 时,
时,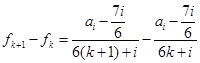
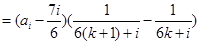
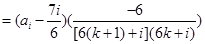
①若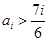 ,则对任意的
,则对任意的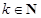 有
有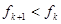 ,数列
,数列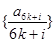 为单调减数列;
为单调减数列;
②若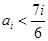 ,则对任意的
,则对任意的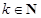 有
有 ,数列
,数列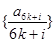 为单调增数列;
为单调增数列;
综上,当 时,数列
时,数列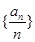 中必有某数重复出现无数次……………14分
中必有某数重复出现无数次……………14分
当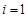 时,
时,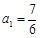 符合要求;当
符合要求;当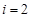 时,
时,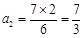 符合要求,此时的
符合要求,此时的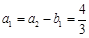 ;
;
当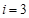 时,
时, 符合要求,此时的
符合要求,此时的 ;
;
当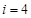 时,
时,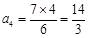 符合要求,此时的
符合要求,此时的 ;
;
当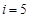 时,
时,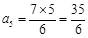 符合要求,此时的
符合要求,此时的 ;
;
当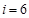 时,
时,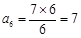 符合要求,此时的
符合要求,此时的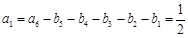 ;
;
即当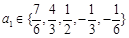 时,数列
时,数列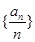 中必有某数重复出现无数次.………………………16分
中必有某数重复出现无数次.………………………16分
(1)当
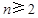 时,有累加法得到
时,有累加法得到
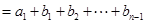
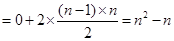 ,
,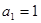 也满足上式,
也满足上式,所以数列
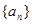 的通项为
的通项为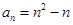 .
. (2)因为
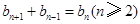 ,
,所以对任意的
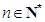 有
有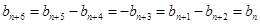 ,
, 所以数列
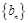 是一个以6为周期的循环数列
是一个以6为周期的循环数列进而证明
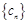 为常数列
为常数列(3)因为
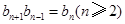 ,且
,且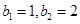 ,所以
,所以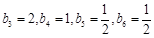 ,
,且对任意的
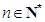 ,有
,有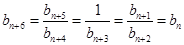 ,
, 设
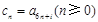 ,(其中
,(其中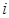 为常数且
为常数且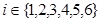 ),所以
),所以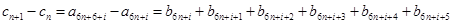
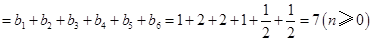 ,
,所以数列
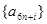 均为以7为公差的等差数列.记
均为以7为公差的等差数列.记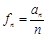 ,构造新数列来分析周期性和最值问题。
,构造新数列来分析周期性和最值问题。(1)当
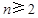 时,有
时,有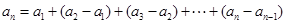
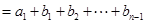 ……………………1分
……………………1分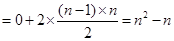 ,
,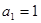 也满足上式,
也满足上式,所以数列
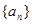 的通项为
的通项为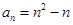 . ………………………………………………………3分
. ………………………………………………………3分(2)因为
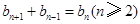 ,
,所以对任意的
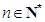 有
有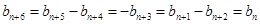 ,
, 所以数列
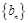 是一个以6为周期的循环数列……………………………………………………5分
是一个以6为周期的循环数列……………………………………………………5分又因为
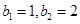 ,所以
,所以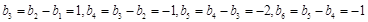
所以
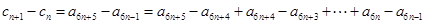

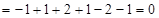
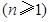 ,
,所以数列
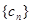 为常数列. ……………………………………………………………………7分
为常数列. ……………………………………………………………………7分(3)因为
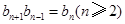 ,且
,且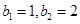 ,所以
,所以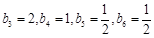 ,
,且对任意的
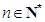 ,有
,有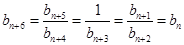 ,
, 设
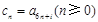 ,(其中
,(其中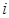 为常数且
为常数且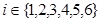 ),所以
),所以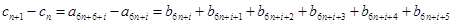
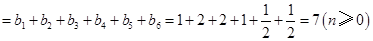 ,
,所以数列
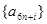 均为以7为公差的等差数列.……………………………………………10分
均为以7为公差的等差数列.……………………………………………10分记
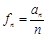 ,则
,则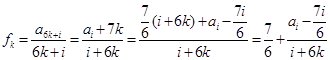 ,
,(其中
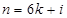
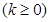 ,
,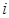 为
为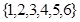 中的一个常数),
中的一个常数),当
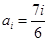 时,对任意的
时,对任意的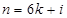 有
有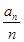
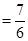 ;…………………………………………12分
;…………………………………………12分当
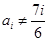 时,
时,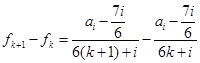
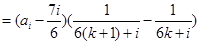
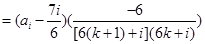
①若
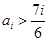 ,则对任意的
,则对任意的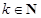 有
有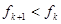 ,数列
,数列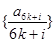 为单调减数列;
为单调减数列;②若
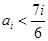 ,则对任意的
,则对任意的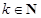 有
有 ,数列
,数列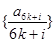 为单调增数列;
为单调增数列; 综上,当
 时,数列
时,数列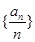 中必有某数重复出现无数次……………14分
中必有某数重复出现无数次……………14分当
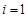 时,
时,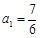 符合要求;当
符合要求;当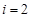 时,
时,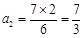 符合要求,此时的
符合要求,此时的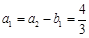 ;
;当
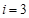 时,
时, 符合要求,此时的
符合要求,此时的 ;
;当
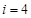 时,
时,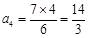 符合要求,此时的
符合要求,此时的 ;
;当
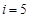 时,
时,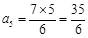 符合要求,此时的
符合要求,此时的 ;
;当
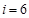 时,
时,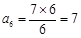 符合要求,此时的
符合要求,此时的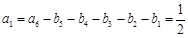 ;
;即当
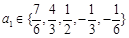 时,数列
时,数列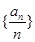 中必有某数重复出现无数次.………………………16分
中必有某数重复出现无数次.………………………16分
练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目

 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )




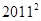 .
.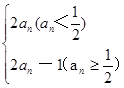 ,若a1=
,若a1=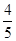 ,则a2012的值为
,则a2012的值为 .
.

 是等和数列,
是等和数列, =3,公和是5,则此数列的前805项的和为 .
=3,公和是5,则此数列的前805项的和为 .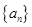 满足
满足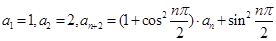 ,则该数列的前10项的和为
,则该数列的前10项的和为  对任意的
对任意的 有
有 ,若
,若 ,则
,则 .
.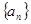 中,
中,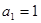 ,
,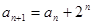 ,则
,则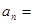 .
.