题目内容
已知等差数列{an}中，a5＝12，a20＝－18.
(1)求数列{an}的通项公式；
(2)求数列{|an|}的前n项和Sn.
(1)求数列{an}的通项公式；
(2)求数列{|an|}的前n项和Sn.
（1）an＝－2n＋22.
（2）Sn＝
（2）Sn＝
解：(1)设数列{an}的公差为d，
依题意得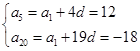
，
解得
，
∴an＝20＋(n－1)×(－2)＝－2n＋22.
(2)由(1)知|an|＝|－2n＋22|＝
，
∴当n≤11时，Sn＝20＋18＋…＋(－2n＋22)＝
＝(21－n)n；
当n>11时，Sn＝S11＋2＋4＋…＋(2n－22)＝110＋
＝n2－21n＋220.
综上所述，Sn＝.
依题意得
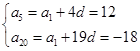，解得
，∴an＝20＋(n－1)×(－2)＝－2n＋22.
(2)由(1)知|an|＝|－2n＋22|＝
，∴当n≤11时，Sn＝20＋18＋…＋(－2n＋22)＝
＝(21－n)n；当n>11时，Sn＝S11＋2＋4＋…＋(2n－22)＝110＋
＝n2－21n＋220.综上所述，Sn＝
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
是等差数列，其中
，前四项和
．
，①求数列
的前
项之和
是不是数列
满足
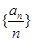是等差数列；
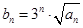，求数列
的前
项和
的前
项和为
且
.
的前
项和
，并求
中，已知
，则
= ( )．