题目内容
已知数列{an}是公差不为0的等差数列,a1=2,且a2,a3,a4+1成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=an+2an,求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)设bn=an+2an,求数列{bn}的前n项和Sn.
(1)an=2n.
(2)Sn=n2+n+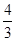 (4n-1).
(4n-1).
(2)Sn=n2+n+
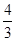 (4n-1).
(4n-1).解:(1)设数列{an}的公差为d,由a1=2和a2,a3,a4+1成等比数列,得
(2+2d)2=(2+d)(3+3d),
解得d=2或d=-1.
当d=-1时,a3=0,与a2,a3,a4+1成等比数列矛盾,舍去.
∴d=2.
∴an=a1+(n-1)d=2+2(n-1)=2n,
即数列{an}的通项公式为an=2n.
(2)∵bn=2n+22n=2n+4n,
∴Sn=(2+41)+(4+42)+…+(2n+4n)=(2+4+…+2n)+(41+42+…+4n)=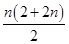 +
+ =n2+n+
=n2+n+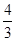 (4n-1).
(4n-1).
(2+2d)2=(2+d)(3+3d),
解得d=2或d=-1.
当d=-1时,a3=0,与a2,a3,a4+1成等比数列矛盾,舍去.
∴d=2.
∴an=a1+(n-1)d=2+2(n-1)=2n,
即数列{an}的通项公式为an=2n.
(2)∵bn=2n+22n=2n+4n,
∴Sn=(2+41)+(4+42)+…+(2n+4n)=(2+4+…+2n)+(41+42+…+4n)=
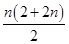 +
+ =n2+n+
=n2+n+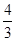 (4n-1).
(4n-1). 
练习册系列答案
相关题目
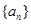 满足
满足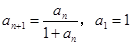 ,归纳出
,归纳出



 -100.
-100.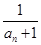 }是等差数列,则a4=( )
}是等差数列,则a4=( )

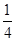
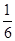
 的前
的前 项和
项和 。
。 的最大或最小值.
的最大或最小值. 是首项为
是首项为 ,公差为
,公差为 的等差数列,
的等差数列, 为其前n项和,若
为其前n项和,若 成等比数列,则
成等比数列,则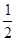

 ,则
,则 ( )
( )


