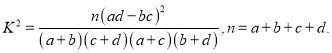��Ŀ����
����Ŀ������������֯�������о�������ʾ��Ŀǰ�й����ӻ����������6�ڣ��������ʹ�ѧ���Ľ����ʾ��ѳ����߳ɣ�Ϊ���о�ÿ���ۼƻ��Ⱪ¶ʱ�䣨��λ��Сʱ������ӷ����ʵĹ�ϵ����ij��ѧһ�꼶200��ѧ�����в������ʾ����飬�õ��������ݣ�
ÿ���ۻ����Ⱪ¶ʱ�䣨��λ��Сʱ�� |
|
|
|
| ������28Сʱ |
�������� | 21 | 39 | 37 | 2 | 1 |
���������� | 3 | 37 | 52 | 5 | 3 |
��1����ÿ���ۼƻ��Ⱪ¶ʱ�䲻����28Сʱ��4��ѧ���У������ȡ2����������ǡ��һ��ѧ�������ӵĸ��ʣ�
��2����ÿ���ۼƻ��Ⱪ¶ʱ������14��Сʱ����֤Ϊ�����㹻�Ļ��Ⱪ¶ʱ�䡱����������������������������������ݣ�2���е��������ж��ܷ��ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ���㹻�Ļ��Ⱪ¶ʱ��������й�ϵ��
���� | ������ | |
�㹻�Ļ��Ⱪ¶ʱ�� | ||
���㹻�Ļ��Ⱪ¶ʱ�� |
��:![]()
P | 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
���𰸡�(1) ![]() (2)������
(2)������
��������
(1)�������⣬ʱ�䲻����28Сʱ��4��ѧ���У�����1����������3��������ǡ��һ�����ӣ�![]() ��4��ѧ����2�����У�
��4��ѧ����2�����У�![]() ��Ȼ����������.
��Ȼ����������.
(2)�ȸ��ݱ���ó��ڻ����ʱ������ӵ������ֱ��Ƕ��٣������������Ȼ����ݹ�ʽ���
![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]() ���ó����.
�����.
��1���衰�����ȡ2��������ǡ��һ��ѧ�������ӡ�Ϊ�¼�![]() ����
����![]()
�������ȡ2��������ǡ��һ��ѧ�������ӵĸ���Ϊ![]() .
.
��2�������������ݵõ���������
���� | ������ | |
�㹻�Ļ��Ⱪ¶ʱ�� | 40 | 60 |
���㹻�Ļ��Ⱪ¶ʱ�� | 60 | 40 |
����![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]() ��
��
�����ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ���㹻�Ļ��Ⱪ¶ʱ��������й�ϵ.

����Ŀ�� 2022�걱�����»�����ɹ�����3�����ϱ�ѩ���ںŵ����������ѩ�������ĿѸ�ٳ�������������ij�ۺϴ�ѧ�ƻ���һ�꼶�������γ̣�Ϊ�˽�ѧ���Ա����˶�����Ȥ������Ӹ�Уһ�꼶ѧ���г�ȡ��100�˽��е��飬����Ů���жԱ����˶�����Ȥ��ռ![]() ����������10�˱�ʾ�Ա����˶�û����Ȥ��
����������10�˱�ʾ�Ա����˶�û����Ȥ��
��1����������![]() �����������ش��ܷ��ڷ�����ĸ��ʲ�����0.1��ǰ������Ϊ���Ա����Ƿ�����Ȥ���Ա��й�����
�����������ش��ܷ��ڷ�����ĸ��ʲ�����0.1��ǰ������Ϊ���Ա����Ƿ�����Ȥ���Ա��й�����
����Ȥ | û��Ȥ | �ϼ� | |
�� | 55 | ||
Ů | |||
�ϼ� |
��2������Ƶ����Ϊ���ʣ����ٴӸ�Уһ�꼶ȫ��ѧ���У�������������ķ���ÿ�γ�ȡ1��ѧ������ȡ5�Σ��DZ���ȡ��5��ѧ���жԱ�������Ȥ������Ϊ![]() ����ÿ�γ�ȡ�Ľ����������ģ���
����ÿ�γ�ȡ�Ľ����������ģ���![]() �ķֲ����������ͷ��
�ķֲ����������ͷ��
������
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072/p> | 2.706 | 3.841 | 5.024 | 6.635 |
�ο���ʽ��