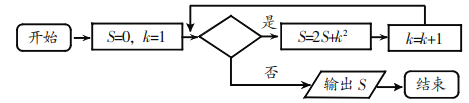
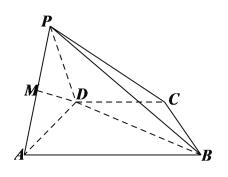
题目内容
【题目】设n为一个正整数,三维空间内的点集S满足下述性质:
(1).空间内不存在n个平面,使得点集S中的每个点至少在这n个平面中的一个平面上;
(2).对于每个点![]() ,均存在n个平面,使得
,均存在n个平面,使得![]() 中的每个点均至少在这n个平面中的一个平面上.
中的每个点均至少在这n个平面中的一个平面上.
求点集S中点的个数的最小值与最大值.
【答案】最小值为3n+1,最大值为![]() .
.
【解析】
先求![]() 的最小可能值.
的最小可能值.
由于过任意三点均可以作一个平面,故![]() .
.
而当3n+1个点中,任意四点不共面时,即满足题设条件.
于是,![]() 的最小可能值为3n+1.
的最小可能值为3n+1.
接下来求![]() 的最大可能值.
的最大可能值.
对于每一个![]() ,
,
设直线![]() 能覆盖
能覆盖![]() .
.
由题设知![]() .
.
设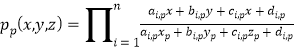 .
.
则![]() 为一个三元n次多项式,且
为一个三元n次多项式,且![]() ,
,![]() .
.
于是,![]() 在
在![]() (
(![]() 为次数不超过n的三元多项式的向量空间)中是线性无关的.
为次数不超过n的三元多项式的向量空间)中是线性无关的.
因此,![]() .
.
下面给出集合S中有![]() 个点的例子.
个点的例子.
如图,设![]() 为
为![]() 个点构成的正四面体点阵.
个点构成的正四面体点阵.
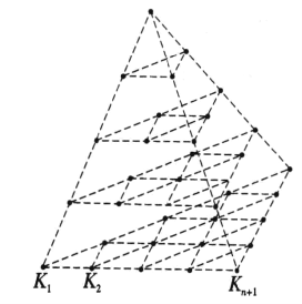
则![]() .
.
对于每个点![]() ,可以用n个平面覆盖
,可以用n个平面覆盖![]() .但不能用n个平面覆盖
.但不能用n个平面覆盖![]() .
.
综上,集合S中点的个数的最大值为![]() .
.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】世界卫生组织的最新研究报告显示,目前中国近视患者人数多达6亿,高中生和大学生的近视率均已超过七成,为了研究每周累计户外暴露时间(单位:小时)与近视发病率的关系,对某中学一年级200名学生进行不记名问卷调查,得到如下数据:
每周累积户外暴露时间(单位:小时) |
|
|
|
| 不少于28小时 |
近视人数 | 21 | 39 | 37 | 2 | 1 |
不近视人数 | 3 | 37 | 52 | 5 | 3 |
(1)在每周累计户外暴露时间不少于28小时的4名学生中,随机抽取2名,求其中恰有一名学生不近视的概率;
(2)若每周累计户外暴露时间少于14个小时被认证为“不足够的户外暴露时间”,根据以上数据完成如下列联表,并根据(2)中的列联表判断能否在犯错误的概率不超过0.01的前提下认为不足够的户外暴露时间与近视有关系?
近视 | 不近视 | |
足够的户外暴露时间 | ||
不足够的户外暴露时间 |
附:![]()
P | 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |