题目内容
【题目】已知椭圆
的两个焦点分别为
，离心率为
.设过点
的直线
与椭圆
相交于不同两点
， 
周长为
.
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知点
，证明：当直线
变化时，总有TA与
的斜率之和为定值．
【答案】（1）
（2）见解析
【解析】试题分析：（Ⅰ）根据题意列出关于
、
、
的方程组，结合性质
， ，求出
、
、
，即可得结果；(II) 当直线
垂直于
轴时，显然直线
与
的斜率之和为0； 当直线不垂直于轴时，设的方程为
与椭圆方程联立，根据两点间的斜率公式及韦达定理将
用参数
表示，化简消去
即可得结论.
试题解析：（Ⅰ）由已知条件得
，所以
椭圆C的标准方程为
（Ⅱ）当直线垂直于轴时，显然直线与的斜率之和为0；
当直线不垂直于轴时，设的方程为
，
与椭圆方程联立得
则
，
，其中
恒成立。
=
=
因为
=
所以
综上：直线与的斜率之和为定值.
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查，得到的统计数据如下表所示：
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
（1）如果随机调查这个班的一名学生，那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少？
（2）若不积极参加班级工作且学习积极性高的7名学生中有两名男生，现从中抽取两名学生参加某项活动，问两名学生中有1名男生的概率是多少？
（3）学生的学习积极性与对待班极工作的态度是否有关系？请说明理由.
附：
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
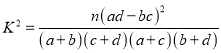
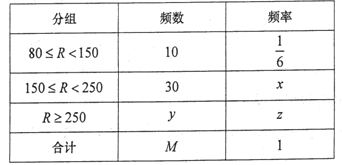
【题目】大家知道， 莫言是中国首位获得诺贝尔奖的文学家， 国人欢欣鼓舞.某高校文学社从男女生中各抽取
名同学调查对莫言作品的了解程度， 结果如下：
阅读过莫言的作品数（ 篇） |
|
|
|
|
|
男生 |
|
|
|
|
|
女生 |
|
|
|
|
|
（1）试估计该校学生阅读莫言作品超过篇的概率；
（2）对莫言作品阅读超过
篇的则称为“对莫言作品非常了解” ， 否则为“ 一般了解” .根据题意完成下表， 并判断能否在犯错误的概率不超过
的前提下， 认为对莫言作品非常了解与性别有关？
非常了解 | 一般了解 | 合计 | |
男生 | |||
女生 | |||
合计 |
附：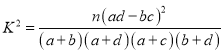
，其中
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】为了研究家用轿车在高速公路上的车速情况，交通部门随机对50名家用轿车驾驶员进行调查，得到其在高速公路上行驶时的平均车速情况为：在30名男性驾驶员中，平均车速超过
的有20人，不超过
的有10人．在20名女性驾驶员中，平均车速超过
的有5人，不超过
的有15人．
（Ⅰ）完成下面的列联表，并判断是否有99.5%的把握认为平均车速超过
的人与性别有关；
平均车速超过
| 平均车速不超过
| 合计 | |
男性驾驶员人数 | |||
女性驾驶员人数 | |||
合计 |
（Ⅱ ）以上述数据样本来估计总体，现从高速公路上行驶的大量家用轿车中随机抽取3辆，记这3辆车中驾驶员为女性且车速不超过
的车辆数为
，若每次抽取的结果是相互独立的，求
的分布列和数学期望．
参考公式： 
，其中
．
参考数据：
| 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
