题目内容
【题目】如图所示,已知边长为![]() 米的正方形钢板有一个角被锈蚀,其中
米的正方形钢板有一个角被锈蚀,其中![]() 米,
米, ![]() 米.为了合理利用这块钢板,将在五边形
米.为了合理利用这块钢板,将在五边形![]() 内截取一个矩形块
内截取一个矩形块![]() ,使点
,使点![]() 在边
在边![]() 上.
上.
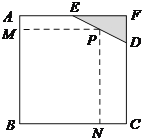
(1)设![]() 米,
米, ![]() 米,将
米,将![]() 表示成
表示成![]() 的函数,求该函数的解析式及定义域;
的函数,求该函数的解析式及定义域;
(2)求矩形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 平方米.
平方米.
【解析】试题分析:(1)利用三角形的相似,可得![]() ,化简即可求得函数的解析式,根据
,化简即可求得函数的解析式,根据![]() 实际意义可得函数的定义域;(2)结合(1)的结论表示出面积,考虑函数定义域的前提下,利用二次函数配方法,可得矩形
实际意义可得函数的定义域;(2)结合(1)的结论表示出面积,考虑函数定义域的前提下,利用二次函数配方法,可得矩形![]() 面积的最大值.
面积的最大值.
试题解析:(1)作PQ⊥AF于Q,所以PQ=8﹣y,EQ=x﹣4
在△EDF中, ![]() ,所以
,所以![]()
所以![]() ,定义域为{x|4≤x≤8}.
,定义域为{x|4≤x≤8}.
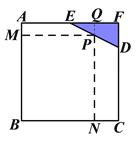
(2)设矩形BNPM的面积为S,则![]()
所以S(x)是关于x的二次函数,且其开口向下,对称轴为x=10
所以当x∈[4,8],S(x)单调递增.
所以,当x=8米时,矩形BNPM面积取得最大值48平方米.

练习册系列答案
相关题目
