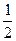题目内容
椭圆过(3,0)点,离心率e=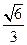 ,求椭圆的标准方程.
,求椭圆的标准方程.
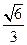 ,求椭圆的标准方程.
,求椭圆的标准方程.椭圆的方程为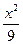 +
+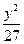 =1或
=1或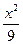 +
+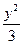 =1.
=1.
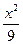 +
+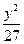 =1或
=1或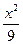 +
+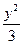 =1.
=1.当椭圆的焦点在x轴上时,
∵a="3,"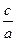 =
=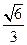 ,
,
∴c=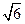 .
.
从而b2=a2-c2=9-6=3,
∴椭圆的方程为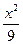 +
+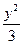 =1.
=1.
当椭圆的焦点在y轴上时,
∵b="3,"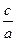 =
=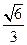 ,
,
∴ =
=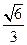 .∴a2=27.
.∴a2=27.
∴椭圆的方程为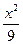 +
+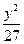 =1.
=1.
∴所求椭圆的方程为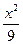 +
+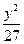 =1或
=1或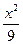 +
+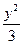 ="1."
="1."
∵a="3,"
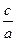 =
=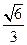 ,
,∴c=
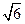 .
.从而b2=a2-c2=9-6=3,
∴椭圆的方程为
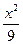 +
+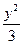 =1.
=1.当椭圆的焦点在y轴上时,
∵b="3,"
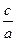 =
=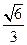 ,
,∴
 =
=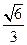 .∴a2=27.
.∴a2=27.∴椭圆的方程为
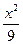 +
+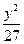 =1.
=1.∴所求椭圆的方程为
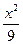 +
+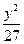 =1或
=1或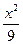 +
+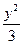 ="1."
="1." 
练习册系列答案
相关题目
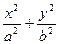 =1的焦点为F1、F2,P是椭圆上任意一点,一条斜率为
=1的焦点为F1、F2,P是椭圆上任意一点,一条斜率为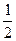 的直线交椭圆于A、B两点,如果当a变化时,总可同时满足:
的直线交椭圆于A、B两点,如果当a变化时,总可同时满足: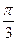 ;
; 的椭圆的一个焦点是(0,4),则此椭圆的准线方程为__________.
的椭圆的一个焦点是(0,4),则此椭圆的准线方程为__________.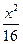 +
+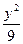 =1或
=1或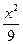 +
+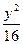 =1
=1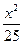 +
+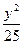 +
+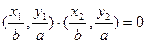 ,椭圆的离心率
,椭圆的离心率 短轴长为2,0为坐标原点.
短轴长为2,0为坐标原点.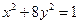 的焦点坐标是( ).
的焦点坐标是( ).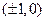
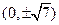
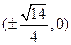
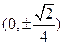
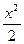 +
+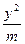 =1的离心率
=1的离心率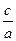 为
为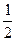 ,则m等于( )
,则m等于( )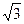
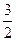
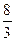
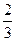
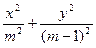 =1的准线平行于x轴,则m应满足的条件是( )
=1的准线平行于x轴,则m应满足的条件是( )