题目内容
【题目】某工厂对一批产品的质量进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图.已知样本中产品净重在[70,75)克的个数是8个. 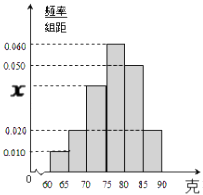
(Ⅰ)求样本容量;
(Ⅱ)若从净重在[60,70)克的产品中任意抽取2个,求抽出的2个产品恰好是净重在[65,70)的产品的概率.
【答案】解:设样本容量为N,由频率分布直方图可知:(0.01+0.02×2+x+0.05+0.06)×5=1 解得:x=0.04,
因为5x= ![]() ,解得N=40;
,解得N=40;
(Ⅱ)由频率分布直方图可知:
净重在[60,65)克的产品有0.01×5×40=2个;净重在[65,70)克的产品有0.02×5×40=4个;
所以净重在[60,70)克的产品有6个.
设净重在[60,65)克的产品编号为a,b;净重在[65,70)×克的4个产品编号为c,d,e,f
则从净重在[60,70)克的产品中任意抽取2个的所有基本事件有15种:
(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(a,b),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f);
其中事件A“抽出的2个产品恰好是净重在[65,70)的产品”包含6个基本事件:
(c,d),(c,e),(c,f),(d,e),(d,f),(e,f);
所以由古典概型知p(A)= ![]()
【解析】(Ⅰ)频率分布直方图的所有正方形的面积和为1,即:(0.01+0.02×2+x+0.05+0.06)×5=1,求出x的值,再根据频率= ![]() 求解即可.量.(Ⅱ)这是一个古典概型,求出所有基本事件的个数,再求出“抽出的2个产品恰好是净重在[65,70)的产品”这个事件包含的基本事件的个数,再求概率即可.
求解即可.量.(Ⅱ)这是一个古典概型,求出所有基本事件的个数,再求出“抽出的2个产品恰好是净重在[65,70)的产品”这个事件包含的基本事件的个数,再求概率即可.

 优等生题库系列答案
优等生题库系列答案【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学同学的成绩如表:
n | 1 | 2 | 3 | 4 | 5 |
x0 | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6及这6位同学成绩的标准差s;
(2)若从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间[68,75)中的概率.