题目内容
【题目】【2016高考四川文科】已知数列{![]() }的首项为1,
}的首项为1,![]() 为数列
为数列![]() 的前n项和,
的前n项和,![]() ,其中q>0,
,其中q>0,![]() .
.
(Ⅰ)若![]() 成等差数列,求
成等差数列,求![]() 的通项公式;
的通项公式;
(Ⅱ)设双曲线![]() 的离心率为
的离心率为![]() ,且
,且![]() ,求
,求![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)已知![]() 的递推式
的递推式![]() ,一般是写出当
,一般是写出当![]() 时,
时,![]() ,两式相减,利用
,两式相减,利用![]() ,得出数列
,得出数列![]() 的递推式,从而证明
的递推式,从而证明![]() 为等比数列,利用等比数列的通项公式得到结论;(Ⅱ)先利用双曲线的离心率定义得到
为等比数列,利用等比数列的通项公式得到结论;(Ⅱ)先利用双曲线的离心率定义得到![]() 的表达式,再由
的表达式,再由![]() 解出
解出![]() 的值,最后利用等比数列的求和公式求解计算.
的值,最后利用等比数列的求和公式求解计算.
试题解析:(Ⅰ)由已知,![]() 两式相减得到
两式相减得到![]() .
.
又由![]() 得到
得到![]() ,故
,故![]() 对所有
对所有![]() 都成立.
都成立.
所以,数列![]() 是首项为1,公比为q的等比数列.
是首项为1,公比为q的等比数列.
从而![]() .
.
由![]() 成等差数列,可得
成等差数列,可得![]() ,所以
,所以![]() ,故
,故![]() .
.
所以![]() .
.
(Ⅱ)由(Ⅰ)可知,![]() .
.
所以双曲线![]() 的离心率
的离心率![]() .
.
由![]() 解得
解得![]() .所以,
.所以,
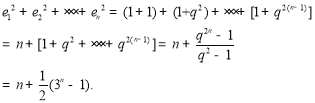 ,
,

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
