题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过抛物线上一点
,过抛物线上一点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断![]() 的形状,并求抛物线
的形状,并求抛物线![]() 的方程;
的方程;
(2)若![]() 两点在抛物线
两点在抛物线![]() 上,且满足
上,且满足![]() ,其中点
,其中点![]() ,若抛物线
,若抛物线![]() 上存在异于
上存在异于![]() 的点
的点![]() ,使得经过
,使得经过![]() 三点的圆和抛物线在点
三点的圆和抛物线在点![]() 处有相同的切线,求点
处有相同的切线,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
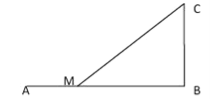
试题分析:(1)设![]() ,则切线
,则切线![]() 的方程为
的方程为![]() ,且
,且![]() ,令
,令![]() ,可得
,可得![]()
![]() 所以
所以![]() 为等腰三角形,且
为等腰三角形,且![]() 为
为![]() 的中点,所以
的中点,所以![]() ,又因
,又因![]() ,求得
,求得![]() ,由此即可求出
,由此即可求出![]() ,进而求出抛物线方程为; (2)由已知,得
,进而求出抛物线方程为; (2)由已知,得![]() 的坐标分别为
的坐标分别为![]() ,设
,设![]() ,求出
,求出![]() 的中垂线方程和
的中垂线方程和![]() 的中垂线方程为
的中垂线方程为![]() ,联立,得圆心坐标为 :
,联立,得圆心坐标为 :![]() ,由
,由![]() ,即可求出
,即可求出![]() ,进而求得
,进而求得![]() 点坐标.
点坐标.
试题解析:(1)设![]() ,
,
则切线![]() 的方程为
的方程为![]() ,且
,且![]() ,
,
所以![]() ,
,
![]() ,所以
,所以![]() ,
,
所以![]() 为等腰三角形,且
为等腰三角形,且![]() 为
为![]() 的中点,
的中点,
所以![]() ,因为
,因为![]() ,
,
所以![]() ,所以
,所以![]() ,得
,得![]() ,
,
所以抛物线方程为![]() ;
;
(2)由已知,得![]() 的坐标分别为
的坐标分别为![]() ,设
,设![]() ,
,
![]() 的中垂线方程为
的中垂线方程为![]() ,①
,①
![]() 的中垂线方程为
的中垂线方程为![]() ,②
,②
联立①②,解得圆心坐标为 :![]() ,
,
由![]() ,得
,得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() 点坐标为
点坐标为![]() .
.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
【题目】某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对![]() 名出租车司机进行调查,调查问卷共
名出租车司机进行调查,调查问卷共![]() 道题,答题情况如下表:
道题,答题情况如下表:
答对题目数 |
|
|
|
|
女 |
|
|
|
|
男 |
|
|
|
|
(I)如果出租车司机答对题目大于等于![]() ,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
(II)从答对题目数小于![]() 的出租车司机中选出
的出租车司机中选出![]() 人做进一步的调查,求选出的
人做进一步的调查,求选出的![]() 人中至少有一名女出租车司机的概率.
人中至少有一名女出租车司机的概率.