题目内容
已知直线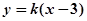 与双曲线
与双曲线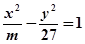 ,有如下信息:联立方程组
,有如下信息:联立方程组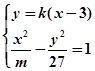 消去
消去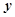 后得到方程
后得到方程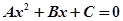 ,分类讨论:(1)当
,分类讨论:(1)当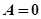 时,该方程恒有一解;(2)当
时,该方程恒有一解;(2)当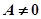 时,
时,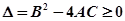 恒成立。在满足所提供信息的前提下,双曲线离心率的取值范围是 ( )
恒成立。在满足所提供信息的前提下,双曲线离心率的取值范围是 ( )
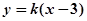 与双曲线
与双曲线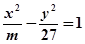 ,有如下信息:联立方程组
,有如下信息:联立方程组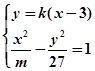 消去
消去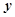 后得到方程
后得到方程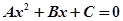 ,分类讨论:(1)当
,分类讨论:(1)当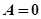 时,该方程恒有一解;(2)当
时,该方程恒有一解;(2)当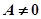 时,
时,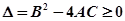 恒成立。在满足所提供信息的前提下,双曲线离心率的取值范围是 ( )
恒成立。在满足所提供信息的前提下,双曲线离心率的取值范围是 ( )A. | B. | C. | D. |
D
先根据直线方程可知直线恒过定点,根据题设条件可知直线与双曲线恒有交点,进而可判断出双曲线的右顶点在定点上或左侧进而求得m的范围,进而根据双曲线方程求得c,进而求得离心率e的表达式,根据m的范围确定e的范围.
解答:解:依题意可知直线恒过定点(3,0),根据(1)和(2)可知直线与双曲线恒有交点,
故需要定点(3,0)在双曲线的右顶点或右顶点的右边,
即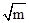 ≤3,求得m≤9
≤3,求得m≤9
要使方程为双曲线需m>0
∴m的范围是0<m≤9
c=
∴e=
∵0<m≤9
∴ ≥2
≥2
即e≥2
故选D.
解答:解:依题意可知直线恒过定点(3,0),根据(1)和(2)可知直线与双曲线恒有交点,
故需要定点(3,0)在双曲线的右顶点或右顶点的右边,
即
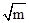 ≤3,求得m≤9
≤3,求得m≤9要使方程为双曲线需m>0
∴m的范围是0<m≤9
c=

∴e=

∵0<m≤9
∴
 ≥2
≥2即e≥2
故选D.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
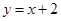 与抛物线
与抛物线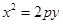 相交于A、B两点,O为原点,若
相交于A、B两点,O为原点,若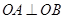 ,
,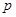 = ( )
= ( )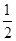 B.1 C.2 D.4
B.1 C.2 D.4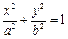
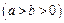 上任意两点
上任意两点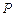 ,
,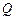 ,若
,若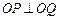 ,则乘积
,则乘积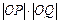 的最小值为 .
的最小值为 . 是双曲线
是双曲线 的左、右焦点,过
的左、右焦点,过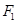 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若
两点,若 为钝角三角形,则该双曲线的离心率
为钝角三角形,则该双曲线的离心率 的取值范围是( )
的取值范围是( )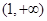



 圆C:
圆C: 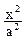 +
+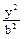 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=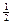 ,且椭圆经过点N(2,-3).
,且椭圆经过点N(2,-3). 与双曲线
与双曲线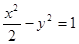 相交于
相交于 两点,则
两点,则 =_________.
=_________.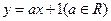 与双曲线
与双曲线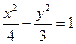 有且仅有一个公共点,求实数
有且仅有一个公共点,求实数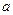 的值.
的值. 的焦距为( )
的焦距为( )



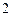 ,函数
,函数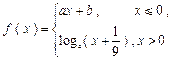 的图象是一条连续不断的曲线,则
的图象是一条连续不断的曲线,则 .
.