题目内容
20.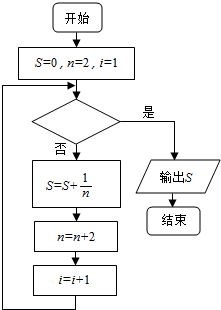 如图给出的是计算12+14+16+18+…+1100的一个程序框图,则判断框内应填入关于i的不等式为( )
如图给出的是计算12+14+16+18+…+1100的一个程序框图,则判断框内应填入关于i的不等式为( )| A. | i<50 | B. | i>50 | C. | i<51 | D. | i>51 |
分析 框图给出的是计算12+14+16+18+…+1100的值的一个程序框图,首先赋值i=1,执行s=0+12时同时执行了i=i+1,和式共有50项作和,所以执行完s=12+14+16+18+…+1100后的i值为51,再判断时i=51应满足条件,由此可以得到正确答案.
解答 解:框图首先给变量s,n,i赋值s=0,n=2,i=1.
判断,条件不满足,执行s=0+12,n=2+2=4,i=1+1=2;
判断,条件不满足,执行s=12+14,n=4+2=6,i=2+1=3;
判断,条件不满足,执行s=12+14+16,n=6+2=8,i=3+1=4;
…
由此看出,当执行s=12+14+16+18+…+1100时,执行n=100+2=102,i=50+1=51.
在判断时判断框中的条件应满足,所以判断框中的条件应是i>50?.
故选:B.
点评 本题考查了程序框图中的直到型循环,虽然是先进行了一次判断,但在不满足条件时执行循环,直到满足条件算法结束,此题是基础题.

练习册系列答案
相关题目
12.已知向量→OA、→OB的夹角为60°,|→OA|=|→OB|=2,若→OC=2→OA+→OB,则|→OC|=( )
| A. | √6 | B. | 2√2 | C. | 2√5 | D. | 2√7 |
11.马路上十盏路灯,为了节约用电可以关掉三盏路灯,但两端两盏不能关掉,也不能同时关掉相邻的两盏或三盏,这样的关灯方法有( )
| A. | 56种 | B. | 36种 | C. | 20种 | D. | 10种 |
5.已知sinθcosθ<0,那么角θ是( )
| A. | 第一或第二象限角 | B. | 第二或第三象限角 | ||
| C. | 第二或第四象限角 | D. | 第一或第四象限角 |
 ,若方程
,若方程 有四个不同的解
有四个不同的解 ,且
,且 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.