题目内容
15.已知函数f(x)=x2-2mx+3.(Ⅰ)当m=1时,求函数f(x)在区间[-2,2]上的最大值和最小值;
(Ⅱ)若函数f(x)在区间[1,+∞)上的值恒为正数,求m的取值范围.
分析 (1)将m=1代入函数的解析式,得到函数的对称轴,从而求出函数的最大值和最小值;
(2)先求出函数的对称轴,通过讨论对称轴的范围结合函数的单调性,从而求出m的范围.
解答 解:(Ⅰ)当m=1时,f(x)=x2-2x+3.
函数f(x)的对称轴是x=1.(2分)
所以在x∈[-2,2]上,当x=时,有最小值f(1)=2;(4分)
当x=-2时,有最大值f(-2)=11.(6分)
(Ⅱ)由已知,函数f(x)的对称轴是x=m.(7分)
①当m≥1时,函数f(x)的最小值为f(m)=3-m2,
若函数f(x)在区间[1,+∞)上的值恒为正数,则3-m2>0,(9分)
解得$-\sqrt{3}<m<\sqrt{3}$,所以$1≤m<\sqrt{3}$;(10分)
②当m<1时,函数f(x)的最小值为f(1)=4-2m,
若函数f(x)在区间[1,+∞)上的值恒为正数,则4-2m>0,(12分)
解得m<2,所以m<1.
综上所述,实数m的取值范围是$(-∞,\sqrt{3})$.(13分)
点评 本题考查了二次函数的性质,考查函数的单调性问题,考查分类讨论,是一道中档题.

练习册系列答案
相关题目
7.已知a为实数,则|a|≥1是关于x的不等式|x-3|+|x-4|≤a有解的(( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.某扇形的半径为1cm,它的周长为4cm,那么该扇形的圆心角为( )
| A. | 2° | B. | 4 | C. | 4° | D. | 2 |
3.将一枚均匀骰子先后投掷两次,得到的点数分别记为a,b,则直线ax+by+5=0与x2+y2=1相切的概率为( )
| A. | $\frac{1}{36}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{9}$ |
10.某高校“统计初步”课程教师随机调查了选该课的一些学生情况,共调查了50人,其中女生27人,男生23人,女生中有20人选统计专业,另外7人选非统计专业;男生中有10人选统计专业,另外13人选非统计专业.
(Ⅰ)根据以上数据完成下列2×2列联表:
(Ⅱ)根据以上数据,能否在犯错误的概率不超过0.05的前提下,认为主修统计专业与性别有关系?
参考数据:附:X2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
当X2≤2.706时,没有充分的证据判定变量A,B有关联,可以认为变量A,B是没有关联的;
当X2>2.706时,有90%的把握判定变量A,B有关联;
当X2>3.814时,有95%的把握判定变量A,B有关联;
当X2>6.635时,有99%的把握判定变量A,B有关联.
(Ⅰ)根据以上数据完成下列2×2列联表:
| 专业 性别 | 非统计专业 | 统计专业 | 总计 |
| 男 | |||
| 女 | |||
| 总计 |
参考数据:附:X2=$\frac{n(ad-bc)^{2}}{(a+c)(b+d)(a+b)(c+d)}$
当X2≤2.706时,没有充分的证据判定变量A,B有关联,可以认为变量A,B是没有关联的;
当X2>2.706时,有90%的把握判定变量A,B有关联;
当X2>3.814时,有95%的把握判定变量A,B有关联;
当X2>6.635时,有99%的把握判定变量A,B有关联.
20.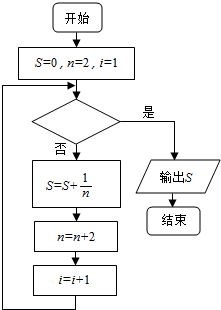 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图,则判断框内应填入关于i的不等式为( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图,则判断框内应填入关于i的不等式为( )
 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图,则判断框内应填入关于i的不等式为( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图,则判断框内应填入关于i的不等式为( )| A. | i<50 | B. | i>50 | C. | i<51 | D. | i>51 |
7.已知cosα=$\frac{3}{5}$,sin β=-$\frac{5}{13}$,且α∈(0,$\frac{π}{2}$),β∈(-$\frac{π}{2}$,0),则sin(α+β)=( )
| A. | $\frac{33}{65}$ | B. | $\frac{63}{65}$ | C. | $\frac{33}{65}$或-$\frac{33}{65}$ | D. | -$\frac{63}{65}$ |
3.一汽车厂生产A、B、C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表(单位:辆):
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.