题目内容
5．已知sinθcosθ＜0，那么角θ是（ ）| A． | 第一或第二象限角 | B． | 第二或第三象限角 | ||
| C． | 第二或第四象限角 | D． | 第一或第四象限角 |
分析 根据题意列出不等式组，由三角函数值的符号判断出θ所在的象限．
解答 解：由题意知，sinθcosθ＜0，
则$\left\{\begin{array}{l}{sinθ＞0}\\{cosθ＜0}\end{array}\right.$或$\left\{\begin{array}{l}{sinθ＜0}\\{cosθ＞0}\end{array}\right.$，所以角θ在第二或第四象限，
故选：C．
点评 本题考查角函数值的符号的应用，需要掌握口诀：一全正、二正弦、三正切、四余弦，属于基础题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
17．$\frac{1}{2}+（{\frac{1}{2}+\frac{1}{4}}）+（{\frac{1}{2}+\frac{1}{4}+\frac{1}{8}}）+…+（{\frac{1}{2}+\frac{1}{4}+…+\frac{1}{{{2^{10}}}}}）$的值为（ ）
| A． | 7+$\frac{1}{2^9}$ | B． | 9+$\frac{1}{{{2^{10}}}}$ | C． | 11+$\frac{1}{{{2^{11}}}}$ | D． | 7+$\frac{1}{{{2^{10}}}}$ |
16．通过随机询问200名性别不同的大学生是否爱好“踢毽子运动”，计算得到统计量值k2的观测值k≈4.892，参照下表，得到的正确结论是（ ）
| P（k2≥k） | 0.10 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
| A． | 在犯错误的概率不超过5%的前提下，认为“爱好该运动与性别有关” | |
| B． | 在犯错误的概率不超过5%的前提下，认为“爱好该运动与性别无关” | |
| C． | 有99%以上的把握认为“爱好该运动与性有关” | |
| D． | 有99%以上的把握认为“爱好该运动与性别无关” |
20．
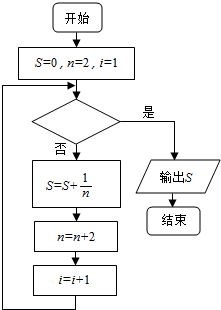如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图，则判断框内应填入关于i的不等式为（ ）
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图，则判断框内应填入关于i的不等式为（ ）| A． | i＜50 | B． | i＞50 | C． | i＜51 | D． | i＞51 |
某校为了了解高三同学暑假期间学习情况，调查了200名同学，统计他们每天平均学习时间，绘成频率分布直方图（如图）．则这200名同学中学习时间在6～8小时的同学为60人．
13．下列说法正确的是（ ）
| A． | 已知购买一张彩票中奖的概率为$\frac{1}{1000}$，则购买1000张这种彩票一定能中奖 | |
| B． | 互斥事件一定是对立事件 | |
| C． | 二进制数1101（2）转化为十进制数是13 | |
| D． | 若样本x1，x2…xn的方差为4，则样本x1-1，x2-1，…，xn-1的方差为3 |
13．已知△ABC的三条边长分别为3，4，5，如果把三角形的三边都增加相同的长度，则这个新三角形的形状为（ ）
| A． | 锐角三角形 | B． | 直角三角形 | ||
| C． | 钝角三角形 | D． | 由增加的长度决定 |