题目内容
12.已知向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为60°,$|\overrightarrow{OA}|=|\overrightarrow{OB}|=2$,若$\overrightarrow{OC}=2\overrightarrow{OA}+\overrightarrow{OB}$,则$|\overrightarrow{OC}|$=( )| A. | $\sqrt{6}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $2\sqrt{7}$ |
分析 由已知求出$\overrightarrow{OC}$2展开,利用数量积计算即可.
解答 解:因为向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为60°,$|\overrightarrow{OA}|=|\overrightarrow{OB}|=2$
所以$\overrightarrow{OA}•\overrightarrow{OB}$=2,
所以${\overrightarrow{OC}}^{2}$=(2$\overrightarrow{OA}+\overrightarrow{OB}$)2=${4\overrightarrow{OA}}^{2}+{\overrightarrow{OB}}^{2}+4\overrightarrow{OA}•\overrightarrow{OB}$=16+4+8=28,
所以$|\overrightarrow{OC}|$=$\sqrt{28}=2\sqrt{7}$;
故选D
点评 本题考查了平面向量的数量积公式的运用求向量的模;一般的,没有坐标表示的向量求模,先求其平方的值,然后开方求模.

练习册系列答案
相关题目
5.以下命题正确的个数是( )
①命题“?x∈R,sinx>0”的否定是“?x∈R,sinx<0”.
②命题“若x2+x-12=0,则x=4”的逆否命题为“若x≠4,则x2+x-12≠0”.
③若p∧q为假命题,则p、q均为假命题.
①命题“?x∈R,sinx>0”的否定是“?x∈R,sinx<0”.
②命题“若x2+x-12=0,则x=4”的逆否命题为“若x≠4,则x2+x-12≠0”.
③若p∧q为假命题,则p、q均为假命题.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
4.现有4种不同品牌的小车各2辆(同一品牌的小车完全相同),计划将其放在4个车库中且每个车库放2辆,则恰有2个车库放的是同一品牌的小车的不同放法共有( )
| A. | 144种 | B. | 108种 | C. | 72种 | D. | 36种 |
1.若f(x)=$\left\{\begin{array}{l}{(1-2a)x+2,x≤1}\\{2{a}^{x},x>1}\end{array}\right.$对任意x1≠x2,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立,那么a的范围是( )
| A. | $(\frac{1}{2},1)$ | B. | $[\frac{3}{4},1)$ | C. | $(\frac{1}{2},\frac{3}{4}]$ | D. | $(0,\frac{3}{4}]$ |
7.已知a为实数,则|a|≥1是关于x的不等式|x-3|+|x-4|≤a有解的(( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.$\frac{1}{2}+({\frac{1}{2}+\frac{1}{4}})+({\frac{1}{2}+\frac{1}{4}+\frac{1}{8}})+…+({\frac{1}{2}+\frac{1}{4}+…+\frac{1}{{{2^{10}}}}})$的值为( )
| A. | 7+$\frac{1}{2^9}$ | B. | 9+$\frac{1}{{{2^{10}}}}$ | C. | 11+$\frac{1}{{{2^{11}}}}$ | D. | 7+$\frac{1}{{{2^{10}}}}$ |
20.若幂函数$y=({{m^2}-5m+7}){x^{{m^2}-6}}$在(0,+∞)单调递增,则实数m值为( )
| A. | 3 | B. | 2 | C. | 2或3 | D. | -2或-3 |
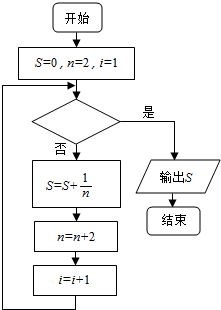 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图,则判断框内应填入关于i的不等式为( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图,则判断框内应填入关于i的不等式为( )