题目内容
11．马路上十盏路灯，为了节约用电可以关掉三盏路灯，但两端两盏不能关掉，也不能同时关掉相邻的两盏或三盏，这样的关灯方法有（ ）| A． | 56种 | B． | 36种 | C． | 20种 | D． | 10种 |
分析 由题意可得：10盏灯关掉其中的3盏灯共有C103=120种方法，再使用插空法解决问题，即先将亮的7盏灯排成一排，所以有6个符合条件的空位，即可得到结论．
解答 解：因为关掉的三盏灯不是两端的灯，且任意两盏都不相邻，
所以我使用插空法解决问题，即先将亮的7盏灯排成一排，
因为两端的灯不能熄灭，
所以有6个符合条件的空位，
所以在6个空位中选取3个位置插入熄灭的3盏灯，即有C63=20种．
故选：C
点评 本题主要考查排列组合的应用，解决此类常用的方法是：特殊元素与特殊位置优先；相邻问题用捆绑的方法；不相邻问题用插空的方法．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
4．现有4种不同品牌的小车各2辆（同一品牌的小车完全相同），计划将其放在4个车库中且每个车库放2辆，则恰有2个车库放的是同一品牌的小车的不同放法共有（ ）
| A． | 144种 | B． | 108种 | C． | 72种 | D． | 36种 |
20．若幂函数$y=（{{m^2}-5m+7}）{x^{{m^2}-6}}$在（0，+∞）单调递增，则实数m值为（ ）
| A． | 3 | B． | 2 | C． | 2或3 | D． | -2或-3 |
6．某扇形的半径为1cm，它的周长为4cm，那么该扇形的圆心角为（ ）
| A． | 2° | B． | 4 | C． | 4° | D． | 2 |
16．通过随机询问200名性别不同的大学生是否爱好“踢毽子运动”，计算得到统计量值k2的观测值k≈4.892，参照下表，得到的正确结论是（ ）
| P（k2≥k） | 0.10 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
| A． | 在犯错误的概率不超过5%的前提下，认为“爱好该运动与性别有关” | |
| B． | 在犯错误的概率不超过5%的前提下，认为“爱好该运动与性别无关” | |
| C． | 有99%以上的把握认为“爱好该运动与性有关” | |
| D． | 有99%以上的把握认为“爱好该运动与性别无关” |
3．将一枚均匀骰子先后投掷两次，得到的点数分别记为a，b，则直线ax+by+5=0与x2+y2=1相切的概率为（ ）
| A． | $\frac{1}{36}$ | B． | $\frac{1}{18}$ | C． | $\frac{1}{12}$ | D． | $\frac{1}{9}$ |
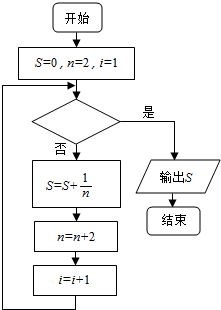如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图，则判断框内应填入关于i的不等式为（ ）