题目内容
8.在△ABC中,角A,B,C的对边分别为a,b,c,cos2C+2cos(A+B)+$\frac{3}{2}$=0,a+b=5,c=$\sqrt{7}$.(1)求角C的大小;
(2)求△ABC的面积.
分析 (1)根据三角形的内角和,得到A+B=π-C,然后结合二倍角公式化简cos2C+2cos(A+B)+$\frac{3}{2}$=0,求出cosC的值,即可求出结果.
(2)利用余弦定理c2=a2+b2-2abcosC,结合条件a+b=5,求出a,b的值,再由三角形的面积公式计算可得.
解答 解:(1)在△ABC中,A+B=π-C,
由已知,得(2cos2C-1)+2cos(π-C)+$\frac{3}{2}$=0,
整理,得4cos2C-4cosC+1=0
解得:cosC=$\frac{1}{2}$,
又∵0<C<180°
∴C=60°;
(2)由余弦定理得:c2=a2+b2-2abcosC,
即($\sqrt{7}$)2=a2+b2-2•abcos60°,①
a+b=5,②
解得b=3,a=2或a=3,b=2.
∴△ABC的面积S=$\frac{1}{2}$absinC=$\frac{1}{2}$×2×3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
点评 本题考查了余弦定理、面积公式以及三角函数的化简,考查运算能力,属于中档题.

练习册系列答案
相关题目
1.若f(x)=$\left\{\begin{array}{l}{(1-2a)x+2,x≤1}\\{2{a}^{x},x>1}\end{array}\right.$对任意x1≠x2,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$<0成立,那么a的范围是( )
| A. | $(\frac{1}{2},1)$ | B. | $[\frac{3}{4},1)$ | C. | $(\frac{1}{2},\frac{3}{4}]$ | D. | $(0,\frac{3}{4}]$ |
20.若幂函数$y=({{m^2}-5m+7}){x^{{m^2}-6}}$在(0,+∞)单调递增,则实数m值为( )
| A. | 3 | B. | 2 | C. | 2或3 | D. | -2或-3 |
16.通过随机询问200名性别不同的大学生是否爱好“踢毽子运动”,计算得到统计量值k2的观测值k≈4.892,参照下表,得到的正确结论是( )
| P(k2≥k) | 0.10 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
| A. | 在犯错误的概率不超过5%的前提下,认为“爱好该运动与性别有关” | |
| B. | 在犯错误的概率不超过5%的前提下,认为“爱好该运动与性别无关” | |
| C. | 有99%以上的把握认为“爱好该运动与性有关” | |
| D. | 有99%以上的把握认为“爱好该运动与性别无关” |
3.将一枚均匀骰子先后投掷两次,得到的点数分别记为a,b,则直线ax+by+5=0与x2+y2=1相切的概率为( )
| A. | $\frac{1}{36}$ | B. | $\frac{1}{18}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{9}$ |
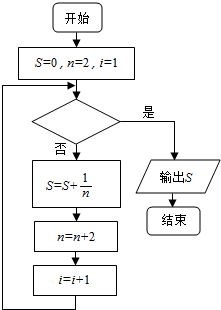 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图,则判断框内应填入关于i的不等式为( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{100}$的一个程序框图,则判断框内应填入关于i的不等式为( ) 某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人.
某校为了了解高三同学暑假期间学习情况,调查了200名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这200名同学中学习时间在6~8小时的同学为60人.