题目内容
已知数列{an}的首项a1=2a+1(a是常数,且a≠-1),
an=2an-1+n2-4n+2(n≥2),数列{bn}的首项b1=a,
bn=an+n2(n≥2).
(1)证明:{bn}从第2项起是以2为公比的等比数列;
(2)设Sn为数列{bn}的前n项和,且{Sn}是等比数列,求实数a的值;
(3)当a>0时,求数列{an}的最小项.
(1)见解析(2)a=- (3)当a∈
(3)当a∈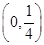 时,最小项为8a-1;当a=
时,最小项为8a-1;当a= 时,最小项为4a或8a-1;当a∈
时,最小项为4a或8a-1;当a∈ 时,最小项为4a;当a=
时,最小项为4a;当a= 时,最小项为4a或2a+1;
时,最小项为4a或2a+1;
当a∈ 时,最小项为2a+1.
时,最小项为2a+1.
解析

练习册系列答案
相关题目
 }中,
}中,
 }是等比数列,并求出数列{
}是等比数列,并求出数列{ 的前n项的和为
的前n项的和为 ,且
,且 ,
,
 是等比数列
是等比数列 与前n项的和
与前n项的和 若集合M=
若集合M= 恰有4个元素,求实数
恰有4个元素,求实数 的取值范围.
的取值范围. 在点
在点 处的切线与
处的切线与 轴的交点坐标为
轴的交点坐标为 .
.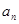 的表达式;
的表达式; ,求数列
,求数列 的前
的前 项和
项和
 ,其前
,其前 项和
项和 满足
满足 且
且 是
是 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; 表示不超过实数
表示不超过实数 的最大整数,记
的最大整数,记 ,求
,求 .
. -
- +
+ +…+
+…+ ,求T2012;
,求T2012;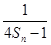 ,Tn为数列{bn}的前n项和,是否存在正整数m(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.
,Tn为数列{bn}的前n项和,是否存在正整数m(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由. 的前n项和为
的前n项和为
 ,
,
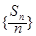 为等差数列;
为等差数列; 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn.