题目内容
4.△ABC的三边长分别为2,3,$\sqrt{19}$,则最大内角为120°.分析 由三边上判断得到$\sqrt{19}$所对的角最大,设为α,利用余弦定理求出cosα的值,即可确定出最大内角.
解答 解:∵△ABC的三边长分别为2,3,$\sqrt{19}$,且$\sqrt{19}$所对的角最大,设为α,
∴cosα=$\frac{{2}^{2}+{3}^{2}-(\sqrt{19})^{2}}{2×2×3}$=-$\frac{1}{2}$,
则α=120°,
故答案为:120°
点评 此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
19.某射击运动员射击一次,命中目标的概率为0.8,问他连续射击两次都没命中的概率为( )
| A. | 0.8 | B. | 0.64 | C. | 0.16 | D. | 0.04 |
13.如图所示的程序框图,若输出的S是62,则①可以为( )
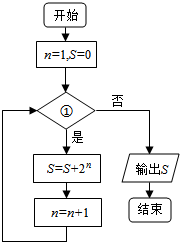

| A. | n≤3? | B. | n≤4? | C. | n≤5? | D. | n≤6? |
14.假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
若由资料知y对x呈线性相关关系.
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程$\widehat{y}$=bx+a的回归系数a,b;$b=\frac{\sum _{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum _{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}},a=\overline{y}-b\overline{x}$
(3)估计使用年限为10年时,维修费用是多少?
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程$\widehat{y}$=bx+a的回归系数a,b;$b=\frac{\sum _{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum _{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}},a=\overline{y}-b\overline{x}$
(3)估计使用年限为10年时,维修费用是多少?
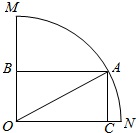 如图:已知扇形MON所在圆半径为1,∠MON=$\frac{π}{2}$,扇形内接矩形ABOC,设∠AON=θ.
如图:已知扇形MON所在圆半径为1,∠MON=$\frac{π}{2}$,扇形内接矩形ABOC,设∠AON=θ.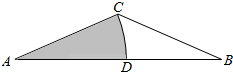 如图,在一个等腰三角形ABC内以A为圆心,腰AC长为半径画弧交底边AB于D,已知AC=1,∠A=30°,现向△ABC内任投一点,该点落在图中阴影部分的概率为$\frac{\sqrt{3}π}{9}$.
如图,在一个等腰三角形ABC内以A为圆心,腰AC长为半径画弧交底边AB于D,已知AC=1,∠A=30°,现向△ABC内任投一点,该点落在图中阴影部分的概率为$\frac{\sqrt{3}π}{9}$.