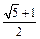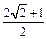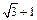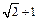题目内容
已知双曲线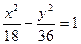 的顶点都是椭圆
的顶点都是椭圆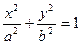 的顶点,直线
的顶点,直线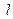 :
: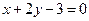 经过椭圆的一个焦点.⑴求椭圆的方程;⑵抛物线
经过椭圆的一个焦点.⑴求椭圆的方程;⑵抛物线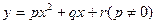 经过椭圆的两个焦点,与直线
经过椭圆的两个焦点,与直线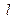 相交于
相交于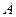 、
、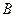 ,试将线段
,试将线段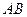 的长
的长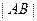 表示为
表示为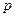 的函数.
的函数.
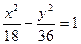 的顶点都是椭圆
的顶点都是椭圆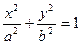 的顶点,直线
的顶点,直线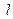 :
: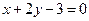 经过椭圆的一个焦点.⑴求椭圆的方程;⑵抛物线
经过椭圆的一个焦点.⑴求椭圆的方程;⑵抛物线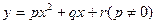 经过椭圆的两个焦点,与直线
经过椭圆的两个焦点,与直线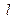 相交于
相交于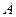 、
、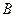 ,试将线段
,试将线段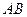 的长
的长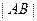 表示为
表示为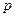 的函数.
的函数.(I)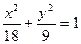 (Ⅱ)
(Ⅱ)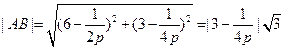
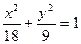 (Ⅱ)
(Ⅱ)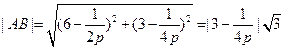
⑴依题意,椭圆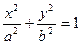 的长轴在
的长轴在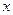 轴上,且
轴上,且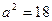 解
解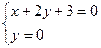 得
得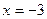 ,从而
,从而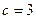 所以
所以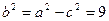 --------5分,所求椭圆的方程为
--------5分,所求椭圆的方程为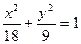
⑵依题意: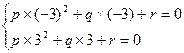 ,解得
,解得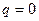 .
.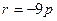 ,所以
,所以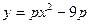
依题意,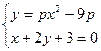 --------10分,解得
--------10分,解得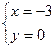 或
或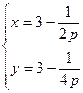
从而 .
.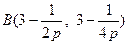
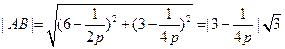
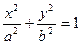 的长轴在
的长轴在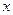 轴上,且
轴上,且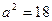 解
解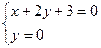 得
得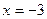 ,从而
,从而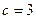 所以
所以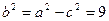 --------5分,所求椭圆的方程为
--------5分,所求椭圆的方程为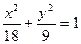
⑵依题意:
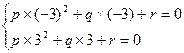 ,解得
,解得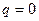 .
.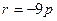 ,所以
,所以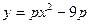
依题意,
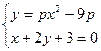 --------10分,解得
--------10分,解得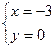 或
或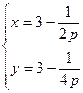
从而
 .
.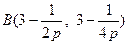
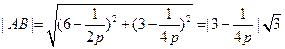

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
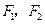 分别是双曲线
分别是双曲线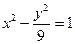 的左、右焦点.若点
的左、右焦点.若点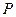 在双曲线上,且
在双曲线上,且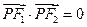 ,则
,则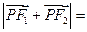 .
.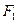 、
、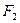 分别是椭圆
分别是椭圆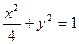 的左、右焦点.
的左、右焦点.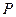 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求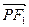 ·
·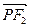 的最大值和最小值;
的最大值和最小值;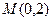 的直线
的直线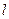 与椭圆交于不同的两点
与椭圆交于不同的两点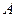 、
、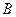 ,且∠
,且∠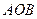 为锐角(其中
为锐角(其中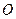 为坐标原点),求直线
为坐标原点),求直线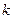 的取值范围.
的取值范围.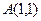 是椭圆
是椭圆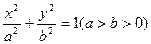 上的一点,
上的一点,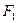 ,
,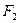 是椭圆的两个焦点,且满足
是椭圆的两个焦点,且满足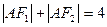 .(Ⅰ)求椭圆的方程及离心率;(Ⅱ)设点
.(Ⅰ)求椭圆的方程及离心率;(Ⅱ)设点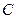 ,
,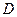 是椭圆上的两点,直线
是椭圆上的两点,直线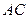 ,
,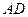 的倾斜角互补,试判断直线
的倾斜角互补,试判断直线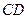 的斜率是否为定值?并说明理由.
的斜率是否为定值?并说明理由.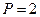 ,又抛物线
,又抛物线 的焦点与双曲线一个焦点重合.
的焦点与双曲线一个焦点重合.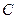 的方程;
的方程;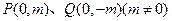 是
是 轴上的两点,过
轴上的两点,过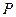 做直线与抛物线
做直线与抛物线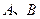 两点,试证:直线
两点,试证:直线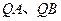 与
与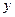 轴所成的锐角相等.
轴所成的锐角相等.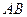 的斜率为1,问
的斜率为1,问 的面积是否有最大值?若有,求出最大值.若没有,说明理由.
的面积是否有最大值?若有,求出最大值.若没有,说明理由.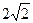 ,其焦点F(c,0)(c>0)对应的准线l与x轴交于A点,|OF|=2|FA|,过A的直线与椭圆交于P、Q两点.
,其焦点F(c,0)(c>0)对应的准线l与x轴交于A点,|OF|=2|FA|,过A的直线与椭圆交于P、Q两点.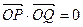 ,求直线PQ的方程; (3)设
,求直线PQ的方程; (3)设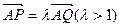 ,过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.
,过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.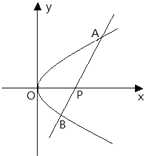
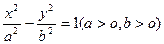 的左焦点F作倾斜角为
的左焦点F作倾斜角为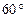 的直线与双曲线相交于A、B两点,若
的直线与双曲线相交于A、B两点,若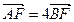 ,则双曲线的离心率为( )
,则双曲线的离心率为( )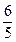 B、
B、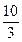 C、
C、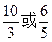 D、2
D、2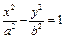 有相同焦点F,点A是两曲线交点,且AF⊥x轴,则双曲线的离心率为 ( )
有相同焦点F,点A是两曲线交点,且AF⊥x轴,则双曲线的离心率为 ( )