题目内容
(13分)已知F1、F2是椭圆c1: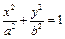 (a>b>0)的左、右焦点,A为右顶点,P为椭圆c1上任意一点,且
(a>b>0)的左、右焦点,A为右顶点,P为椭圆c1上任意一点,且 最大值的取值范围是[c2,3c2],c2=a2-b2.(1)求椭圆c1离心率e的取值范围;(2)设双曲线c2以椭圆c1焦点为顶点,顶点为焦点,B是双曲线c2在第一象限上任意一点,当椭圆c1离心率e取得最小值时,问是否存在正常数λ使∠BAF1=λ∠BF1A恒成立?若存在,求出λ值;若不存在,请说明理由.
最大值的取值范围是[c2,3c2],c2=a2-b2.(1)求椭圆c1离心率e的取值范围;(2)设双曲线c2以椭圆c1焦点为顶点,顶点为焦点,B是双曲线c2在第一象限上任意一点,当椭圆c1离心率e取得最小值时,问是否存在正常数λ使∠BAF1=λ∠BF1A恒成立?若存在,求出λ值;若不存在,请说明理由.
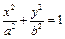 (a>b>0)的左、右焦点,A为右顶点,P为椭圆c1上任意一点,且
(a>b>0)的左、右焦点,A为右顶点,P为椭圆c1上任意一点,且 最大值的取值范围是[c2,3c2],c2=a2-b2.(1)求椭圆c1离心率e的取值范围;(2)设双曲线c2以椭圆c1焦点为顶点,顶点为焦点,B是双曲线c2在第一象限上任意一点,当椭圆c1离心率e取得最小值时,问是否存在正常数λ使∠BAF1=λ∠BF1A恒成立?若存在,求出λ值;若不存在,请说明理由.
最大值的取值范围是[c2,3c2],c2=a2-b2.(1)求椭圆c1离心率e的取值范围;(2)设双曲线c2以椭圆c1焦点为顶点,顶点为焦点,B是双曲线c2在第一象限上任意一点,当椭圆c1离心率e取得最小值时,问是否存在正常数λ使∠BAF1=λ∠BF1A恒成立?若存在,求出λ值;若不存在,请说明理由.(1)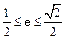 (2)λ=2
(2)λ=2
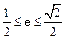 (2)λ=2
(2)λ=2(1)设P(x,y),则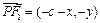 ,
,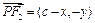 .∴
.∴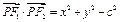 ,将
,将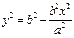 代入得
代入得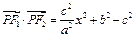 ,0≤x2≤a2,当x2=a2时得
,0≤x2≤a2,当x2=a2时得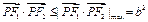 ,又c2≤b2≤3c2,即c2≤a2-c2≤3c2,∴
,又c2≤b2≤3c2,即c2≤a2-c2≤3c2,∴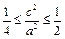 .∴
.∴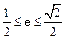 .
.
(2)当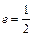 时,a=2c,b=
时,a=2c,b=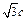 ,∴
,∴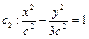 ,A(2c,0).设B(x0,y0),(x0,y0>0),则
,A(2c,0).设B(x0,y0),(x0,y0>0),则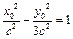 ,当AB⊥x轴时,则
,当AB⊥x轴时,则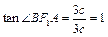 ,∴
,∴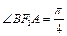 ,故
,故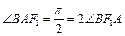 .由此猜想λ=2可使
.由此猜想λ=2可使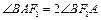 总成立,证明如下:
总成立,证明如下:
当x0≠2c时,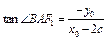 ,
,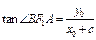 ,∴
,∴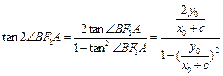 ,
,
将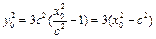 代入得
代入得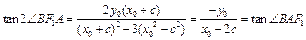 .
.
又∵2∠BF1A与∠BAF1同在区间(0, )∪(
)∪(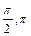 )内,∴2∠BF1A=∠BAF1.
)内,∴2∠BF1A=∠BAF1.
故存在λ=2,使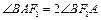 恒成立.
恒成立.
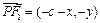 ,
,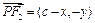 .∴
.∴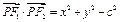 ,将
,将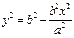 代入得
代入得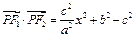 ,0≤x2≤a2,当x2=a2时得
,0≤x2≤a2,当x2=a2时得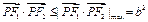 ,又c2≤b2≤3c2,即c2≤a2-c2≤3c2,∴
,又c2≤b2≤3c2,即c2≤a2-c2≤3c2,∴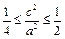 .∴
.∴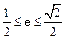 .
.(2)当
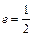 时,a=2c,b=
时,a=2c,b=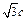 ,∴
,∴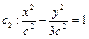 ,A(2c,0).设B(x0,y0),(x0,y0>0),则
,A(2c,0).设B(x0,y0),(x0,y0>0),则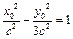 ,当AB⊥x轴时,则
,当AB⊥x轴时,则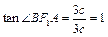 ,∴
,∴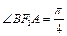 ,故
,故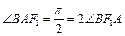 .由此猜想λ=2可使
.由此猜想λ=2可使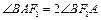 总成立,证明如下:
总成立,证明如下:当x0≠2c时,
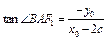 ,
,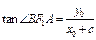 ,∴
,∴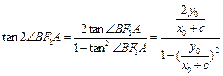 ,
,将
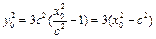 代入得
代入得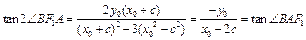 .
.又∵2∠BF1A与∠BAF1同在区间(0,
 )∪(
)∪(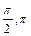 )内,∴2∠BF1A=∠BAF1.
)内,∴2∠BF1A=∠BAF1.故存在λ=2,使
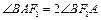 恒成立.
恒成立.
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
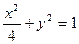 ,过B(-1,0)的直线l交随圆于C、D两点,交直线x=-4于E点,B、E分
,过B(-1,0)的直线l交随圆于C、D两点,交直线x=-4于E点,B、E分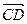 的比分λ1、λ2.求证:λ1+λ2=0
的比分λ1、λ2.求证:λ1+λ2=0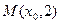 发出的光线沿平行于抛物线
发出的光线沿平行于抛物线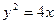 的轴的方向射向此抛物线上的点P,反射后经焦点F又射向抛物线上的点Q,再反射后沿平行于抛物线的轴的方向射向直线
的轴的方向射向此抛物线上的点P,反射后经焦点F又射向抛物线上的点Q,再反射后沿平行于抛物线的轴的方向射向直线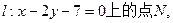 再反射后又射回点M,则 x0= .
再反射后又射回点M,则 x0= .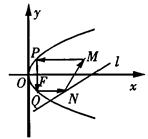
 已知
已知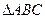 的三边长
的三边长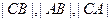 成等差数列,若点
成等差数列,若点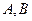 的坐标分别为
的坐标分别为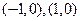 .(1)求顶点
.(1)求顶点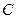 的轨迹
的轨迹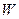 的方程;
的方程;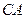 的延长线交轨迹
的延长线交轨迹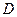 ,当
,当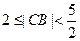 时求线段
时求线段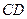 的垂直平分线
的垂直平分线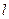 与
与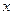 轴交点的横坐标的取值范围.
轴交点的横坐标的取值范围.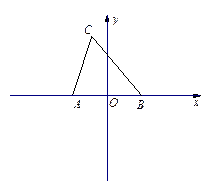
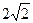 ,其焦点F(c,0)(c>0)对应的准线l与x轴交于A点,|OF|=2|FA|,过A的直线与椭圆交于P、Q两点.
,其焦点F(c,0)(c>0)对应的准线l与x轴交于A点,|OF|=2|FA|,过A的直线与椭圆交于P、Q两点.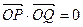 ,求直线PQ的方程; (3)设
,求直线PQ的方程; (3)设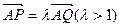 ,过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.
,过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线. 上任意一点到两焦点距离之和为4,直线
上任意一点到两焦点距离之和为4,直线 为该椭圆的一条准线.
为该椭圆的一条准线. 与椭圆C交于不同的两点
与椭圆C交于不同的两点 且
且 (其中
(其中 为坐标原点),求直线
为坐标原点),求直线 的斜率
的斜率 的取值范围.
的取值范围.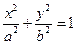 (a>b>0)的左右顶点,P为直线x=u上不同于(u,0)的任一点,若直线AP、BP分别与椭圆交于异于A、B的点M、N,研究点B与以MN为直径的圆的位置关系.
(a>b>0)的左右顶点,P为直线x=u上不同于(u,0)的任一点,若直线AP、BP分别与椭圆交于异于A、B的点M、N,研究点B与以MN为直径的圆的位置关系.