题目内容
已知数列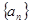 的前n项和为
的前n项和为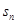 ,且
,且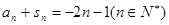 。
。
(1)证明:数列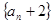 是等比数列;
是等比数列;
(2)若数列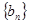 满足
满足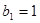 ,且
,且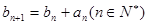 ,求数列
,求数列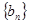 的通项公式。
的通项公式。
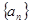 的前n项和为
的前n项和为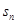 ,且
,且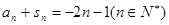 。
。(1)证明:数列
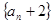 是等比数列;
是等比数列;(2)若数列
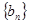 满足
满足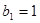 ,且
,且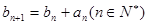 ,求数列
,求数列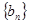 的通项公式。
的通项公式。(1)见解析(2)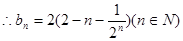
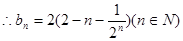
本题主要考查函数,导数,不等式等基础知识,同时考查综合运用数学知识进行推理论证的能立,以及函数与方程和特殊与一般的思想.
(I) 利用曲线y=f(x)与y=g(x)在点(2,0)处有相同的切线l,可得f(2)=g(2)=0,f'(2)=g'(2)=1.即为关于a、b的方程,解方程即可.
(2)由(1)知通项公式,然后借助数列的关系式得到结论。
证明:(1)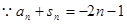
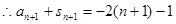
两式相减得: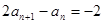
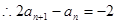
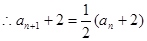
即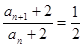
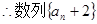 是公比
是公比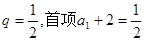 的等比数列。
的等比数列。
(2)由(1)知: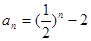
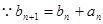
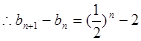
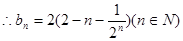
(I) 利用曲线y=f(x)与y=g(x)在点(2,0)处有相同的切线l,可得f(2)=g(2)=0,f'(2)=g'(2)=1.即为关于a、b的方程,解方程即可.
(2)由(1)知通项公式,然后借助数列的关系式得到结论。
证明:(1)
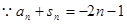
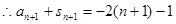
两式相减得:
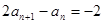
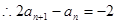
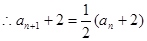
即
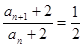
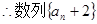 是公比
是公比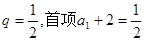 的等比数列。
的等比数列。(2)由(1)知:
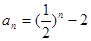
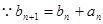
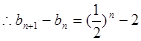
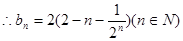

练习册系列答案
相关题目
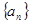 中,
中, 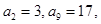 求
求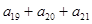 的值。
的值。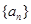 的前
的前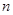 项和为
项和为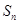 .若
.若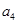 是
是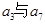 的等比中项,S10="60" ,则S20等于 _________
的等比中项,S10="60" ,则S20等于 _________ 
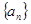 中,
中,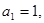 且点
且点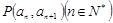 在直线
在直线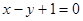 上.
上.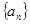 的通项公式;
的通项公式; (2)若函数
(2)若函数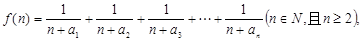 求函数
求函数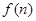 的最小值;
的最小值;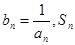 表示数列
表示数列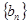 的前
的前 项和.试问:是否存在关于
项和.试问:是否存在关于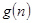 ,使得
,使得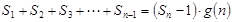 对于一切不小于2的自然数
对于一切不小于2的自然数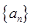 满足
满足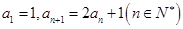
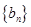 满足
满足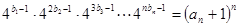 ,求数列
,求数列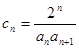 ,求数列
,求数列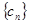 的前n项和
的前n项和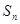
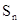 ,若
,若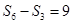 ,则
,则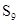 =____________.
=____________.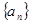 的前n项和,若
的前n项和,若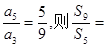 ( )
( )