题目内容
(本小题满分16分)
已知数列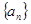 中,
中,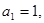 且点
且点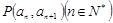 在直线
在直线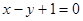 上.
上.
(1)求数列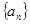 的通项公式;
的通项公式;
 (2)若函数
(2)若函数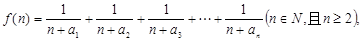 求函数
求函数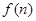 的最小值;
的最小值;
(3)设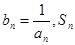 表示数列
表示数列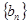 的前
的前 项和.试问:是否存在关于
项和.试问:是否存在关于 的整式
的整式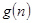 ,使得
,使得
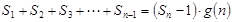 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立? 若存在,写出
恒成立? 若存在,写出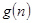 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
已知数列
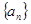 中,
中,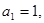 且点
且点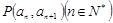 在直线
在直线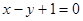 上.
上.(1)求数列
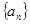 的通项公式;
的通项公式; (2)若函数
(2)若函数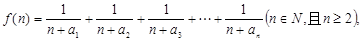 求函数
求函数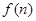 的最小值;
的最小值;(3)设
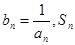 表示数列
表示数列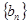 的前
的前 项和.试问:是否存在关于
项和.试问:是否存在关于 的整式
的整式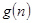 ,使得
,使得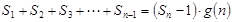 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立? 若存在,写出
恒成立? 若存在,写出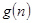 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.(1)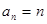 ;(2)
;(2)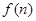 的最小值是
的最小值是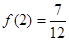 ;
;
(3)存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立。
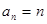 ;(2)
;(2)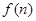 的最小值是
的最小值是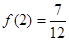 ;
;(3)存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立。
(1)由点P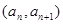 在直线
在直线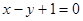 上,可得
上,可得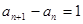 ,从而确定{
,从而确定{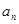 }是以1为首项,1为公差的等差数列.可得其通项公式.
}是以1为首项,1为公差的等差数列.可得其通项公式.
(2)根据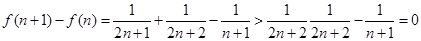 ,得到f(n)是单调增数列,从而最小值为f(2).
,得到f(n)是单调增数列,从而最小值为f(2).
(3)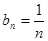 ,可得
,可得 ,
,
然后解本小题关键是把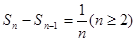 转化为
转化为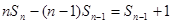 .
.
(1)由点P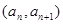 在直线
在直线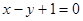 上,
上,
即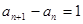 , ----------------2分
, ----------------2分
且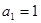 ,数列{
,数列{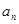 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列
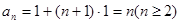 ,
,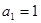 同样满足,所以
同样满足,所以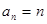 ---------------4分
---------------4分
(2)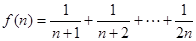
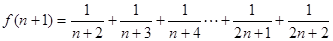 ---------------------6分
---------------------6分
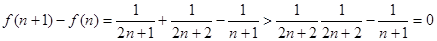
所以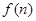 是单调递增,故
是单调递增,故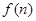 的最小值是
的最小值是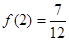 -----------------------10分
-----------------------10分
(3)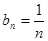 ,可得
,可得 ,
,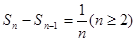 -------12分
-------12分
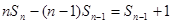 ,
,
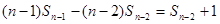
……
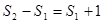
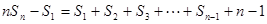
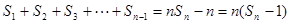 ,n≥2------------------14分
,n≥2------------------14分
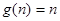
故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立----16分
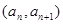 在直线
在直线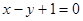 上,可得
上,可得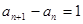 ,从而确定{
,从而确定{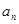 }是以1为首项,1为公差的等差数列.可得其通项公式.
}是以1为首项,1为公差的等差数列.可得其通项公式.(2)根据
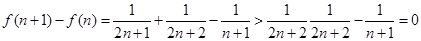 ,得到f(n)是单调增数列,从而最小值为f(2).
,得到f(n)是单调增数列,从而最小值为f(2).(3)
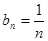 ,可得
,可得 ,
,然后解本小题关键是把
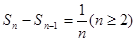 转化为
转化为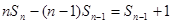 .
.(1)由点P
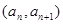 在直线
在直线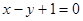 上,
上,即
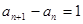 , ----------------2分
, ----------------2分且
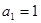 ,数列{
,数列{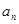 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列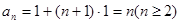 ,
,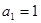 同样满足,所以
同样满足,所以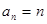 ---------------4分
---------------4分(2)
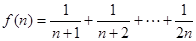
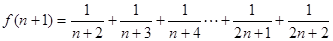 ---------------------6分
---------------------6分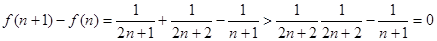
所以
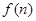 是单调递增,故
是单调递增,故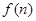 的最小值是
的最小值是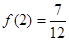 -----------------------10分
-----------------------10分(3)
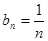 ,可得
,可得 ,
,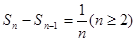 -------12分
-------12分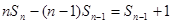 ,
,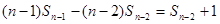
……
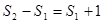
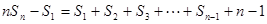
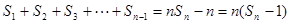 ,n≥2------------------14分
,n≥2------------------14分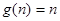
故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立----16分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
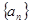 的前n项和为
的前n项和为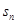 ,且
,且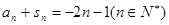 。
。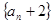 是等比数列;
是等比数列;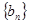 满足
满足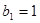 ,且
,且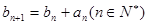 ,求数列
,求数列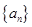 的公比
的公比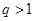 ,
, 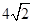 是
是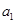 和
和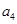 的一个等比中项,
的一个等比中项,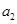 和
和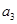 的等差中项为
的等差中项为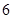 ,若数列
,若数列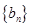 满足
满足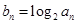 (
(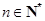 ).
).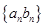 的前
的前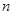 项和
项和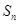 .
.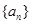 是递增数列,且满足
是递增数列,且满足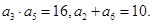
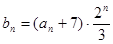 ,求数列
,求数列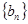 的前
的前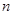 项和
项和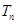 .
.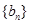 的前
的前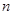 项和为
项和为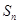 ,且
,且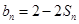 ;数列
;数列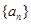 为等差数列,且
为等差数列,且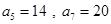 .
.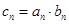 (
(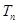 为数列
为数列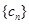 的前
的前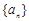 、
、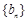 的前
的前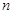 项和分别为
项和分别为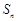 、
、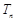 ,对任意的
,对任意的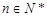 都有
都有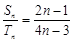 ,则
,则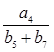
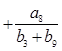 =
= 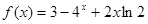 ,数列{an}满足:
,数列{an}满足: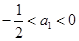 ,
,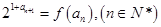 .
.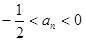
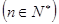 ;
;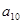 等于( )
等于( )