题目内容
如图所示,在四棱锥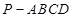 中,底面
中,底面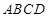 为矩形,
为矩形,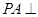 平面
平面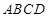 ,点
,点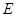 在线段
在线段 上,
上,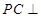 平面
平面 .
.
(1)证明: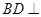 平面
平面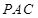 .;
.;
(2)若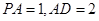 ,求三棱锥
,求三棱锥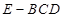 的体积.
的体积.
(1)见解析(2)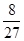
解析试题分析:(1)要证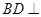 平面
平面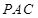 ,需证
,需证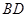 与平面
与平面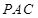 内的两条相交直线都垂直,
内的两条相交直线都垂直,
由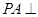 平面
平面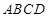 ,可证
,可证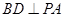 ,由
,由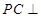 平面
平面 ,可证
,可证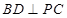 .根据线面垂直的判定定理,
.根据线面垂直的判定定理,
可证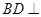 平面
平面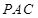 .(2)设矩形
.(2)设矩形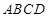 的对角线的交点为
的对角线的交点为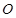 ,连结
,连结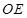 ,由(1)的结论可知
,由(1)的结论可知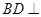 平面
平面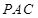 ,从而有
,从而有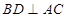 ,所以矩形
,所以矩形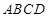 为正方形,边长为2;由
为正方形,边长为2;由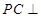 平面
平面 ,知
,知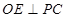 ,因此
,因此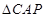 与
与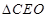 相似,可确定
相似,可确定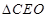 的各边长,然后由
的各边长,然后由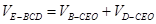 求三棱锥
求三棱锥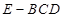 的体积.
的体积.
试题解析:(1)∵PA⊥平面ABCD,
∴PA⊥BD.
∵PC⊥平面BDE,
∴PC⊥BD.
又PA∩PC=P,∴BD⊥平面PAC. 6分
(2)如图,设AC与BD的交点为O,连结OE.
∵PC⊥平面BDE,∴PC⊥OE.
由(1)知,BD⊥平面PAC,∴BD⊥AC,
由题设条件知,四边形ABCD为正方形.
由AD=2,得AC=BD=2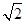 ,OC=
,OC=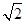 .
.
在Rt△PAC中,PC=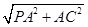 =
=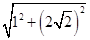 =3.
=3.
易知Rt△PAC∽Rt△OEC,
∴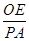 =
=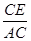 =
=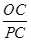 ,即
,即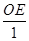 =
=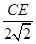 =
=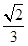 ,∴OE=
,∴OE=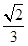 ,CE=
,CE=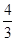 .
.
∴VE-BCD=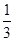 S△CEO·BD=
S△CEO·BD=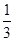 ·
·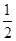 OE·CE·BD=
OE·CE·BD=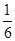 ·
·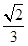 ·
·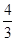 ·2
·2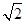 =
=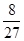 . 13分
. 13分
考点:1、直线与平面垂直的判定与性质;2、棱锥的体积.

练习册系列答案
相关题目

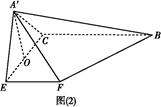
 A′BC的体积.
A′BC的体积.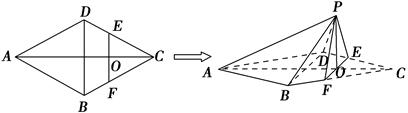
 ,求此时线段PO的长.
,求此时线段PO的长.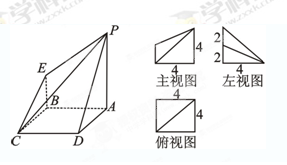
 为
为 的中点,求证:
的中点,求证: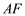
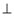 面
面 ;
; 面
面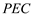 .
.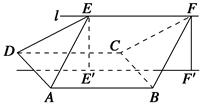
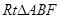 中,AB=2BF=4,C,E分别是AB,AF的中点(如下左图).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如下右图),已知D是AB的中点.
中,AB=2BF=4,C,E分别是AB,AF的中点(如下左图).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如下右图),已知D是AB的中点.
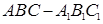 中,
中,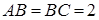 ,
,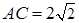 ,
,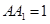 ,D为BC的中点.
,D为BC的中点.
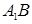 ∥面
∥面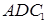 ;
; 的体积.
的体积.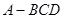 的底面边长为
的底面边长为 ,侧棱长为
,侧棱长为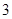 ,
,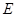 为棱
为棱 的中点.
的中点.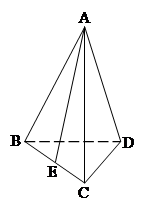
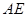 与
与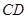 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);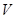 .
.