题目内容
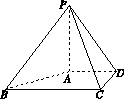
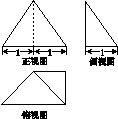
如图(1)所示,△ABC是等腰直角三角形,AC=BC=4,E、F分别为AC、AB的中点,将△AEF沿EF折起,使A′在平面BCEF上的射影O恰为EC的中点,得到图(2).
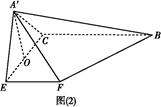
(1)求证:EF⊥A′C;
(2)求三棱锥F A′BC的体积.
A′BC的体积.
(1)见解析 (2) 
解析(1)证明:在△ABC中,EF是等腰直角△ABC的中位线,
∴EF⊥AC,
在四棱锥A′ BCEF中,EF⊥A′E,EF⊥EC,
BCEF中,EF⊥A′E,EF⊥EC,
又EC∩A′E=E,∴EF⊥平面A′EC,
又A′C?平面A′EC,
∴EF⊥A′C.
(2)解:在直角梯形BCEF中,EC=2,BC=4,
∴S△FBC=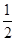 BC·EC=4,
BC·EC=4,
∵A′O⊥平面BCEF,
∴A′O⊥EC,
又∵O为EC的中点,
∴△A′EC为正三角形,边长为2,
∴A′O= ,
,
∴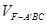 =
=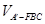 =
=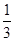 S△FBC·A′O=
S△FBC·A′O=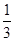 ×4×
×4× =
= .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 的底面
的底面 是边长为
是边长为 的正方形,高
的正方形,高 ,
, 为
为 的中点,
的中点, 与
与 交于
交于 点.
点.  平面
平面 ;
; ∥平面
∥平面 ;
; 的体积.
的体积.
 中,
中, 是等边三角形,
是等边三角形, .
.
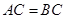 ;
; ;
; ,且平面
,且平面 平面
平面 ,求三棱锥
,求三棱锥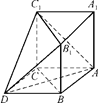

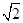 ,∠CDA=45°,求四棱锥P-ABCD的体积.
,∠CDA=45°,求四棱锥P-ABCD的体积.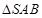 ,
,  为底面圆周上一点.
为底面圆周上一点.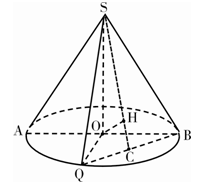
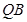 的中点为
的中点为 ,
,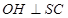 ,求证
,求证 平面
平面 ;
;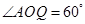 ,
,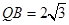 ,求此圆锥的全面积.
,求此圆锥的全面积. ,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
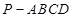 中,底面
中,底面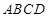 为矩形,
为矩形,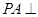 平面
平面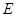 在线段
在线段 上,
上,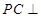 平面
平面 .
.
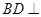 平面
平面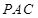 .;
.;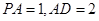 ,求三棱锥
,求三棱锥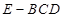 的体积.
的体积.