题目内容
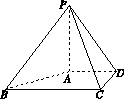
如图,正三棱锥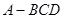 的底面边长为
的底面边长为 ,侧棱长为
,侧棱长为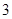 ,
,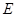 为棱
为棱 的中点.
的中点.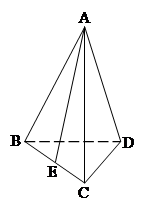
(1)求异面直线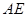 与
与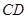 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)求该三棱锥的体积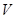 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)求异面直线所成的角,一般是按照定义作出这个角,即作平行线,把空间角化为平面角,通过解三角形来处理,而作平行线,一般都是过异面直线中一条上的某点作一条的平行线,如本题中有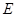 是
是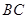 的中点,我们只要取
的中点,我们只要取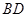 中点
中点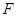 ,则就有
,则就有 ∥
∥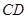 ,
,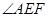 (或其补角)就是所求;(2)要求棱锥体积,就要求出底面积(本题底面是正三角形,面积易求)和高,正棱锥中我们知道棱锥的高,侧棱,侧棱在底面上的射影构成一个直角三角形,可在这个直角三角形中求出正棱锥的高.
(或其补角)就是所求;(2)要求棱锥体积,就要求出底面积(本题底面是正三角形,面积易求)和高,正棱锥中我们知道棱锥的高,侧棱,侧棱在底面上的射影构成一个直角三角形,可在这个直角三角形中求出正棱锥的高.
试题解析:(1)取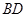 中点
中点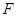 ,连结
,连结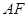 、
、 ,因为
,因为 ∥
∥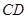 ,所以
,所以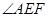 就是异面直线
就是异面直线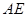 与
与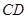 所成的角(或其补角). (2分)
所成的角(或其补角). (2分)
在△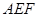 中,
中,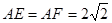 ,
,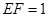 , (1分)
, (1分)
所以 . (2分)
. (2分)
所以,异面直线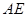 与
与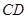 所成的角的大小为
所成的角的大小为 . (1分)
. (1分)
(2)作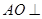 平面
平面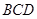 ,则
,则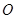 是正△
是正△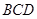 的中心, (1分)
的中心, (1分)
连结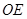 ,
, , (1分)
, (1分)
所以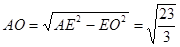 , (1分)
, (1分)
所以,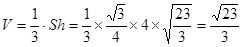 . (2分)
. (2分)
考点:(1)异面直线所成的角;(2)棱锥的体积.

练习册系列答案
相关题目
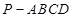 中,底面
中,底面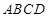 为矩形,
为矩形,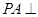 平面
平面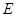 在线段
在线段 上,
上,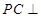 平面
平面 .
.
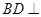 平面
平面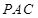 .;
.;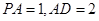 ,求三棱锥
,求三棱锥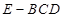 的体积.
的体积.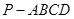 中,底面
中,底面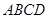 是菱形,
是菱形,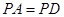 ,
,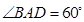 ,
,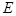 是
是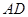 的中点,点
的中点,点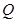 在侧棱
在侧棱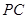 上.
上.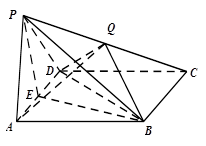
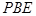 ;
; //平面
//平面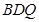 ;
;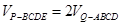 ,试求
,试求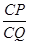 的值.
的值. 平面
平面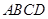 ,四边形
,四边形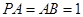 ,
,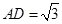 ,点
,点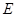 ,
,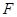 分别是
分别是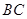 ,
,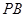 的中点.
的中点.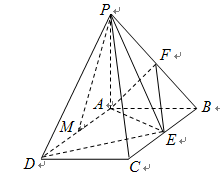
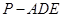 的体积;
的体积; 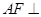 平面
平面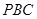 ;
;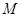 为线段
为线段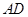 中点,求证:
中点,求证: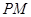 ∥平面
∥平面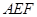 .
.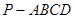 中,
中,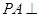 平面
平面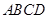 ,底面
,底面 是平行四边形,
是平行四边形,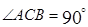 ,
,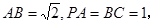
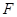 是
是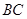 的中点
的中点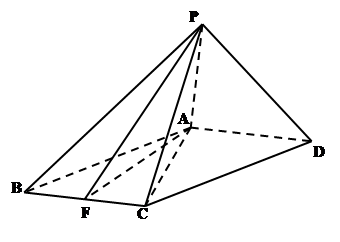
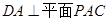
 上确定一点
上确定一点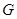 ,使
,使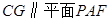 ,求三棱锥
,求三棱锥 的体积.
的体积. 的棱长为
的棱长为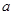 .
.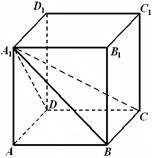
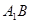 与
与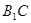 所成角的大小;
所成角的大小;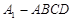 的体积.
的体积.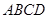 中
中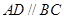 ,
,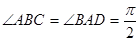 ,
,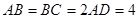 ,
,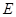 、
、 分别是
分别是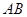 、
、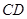 上的点,
上的点,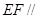
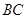 ,
,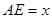 .沿
.沿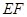 将梯形
将梯形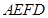 翻折,使平面
翻折,使平面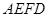 ⊥平面
⊥平面 (如图).
(如图). 是
是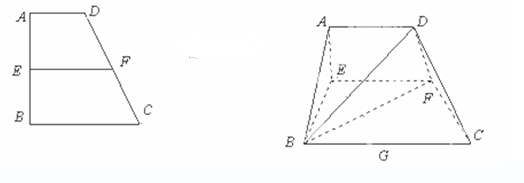
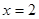 时,求证:
时,求证: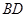 ⊥
⊥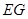 ;
; 变化时,求三棱锥
变化时,求三棱锥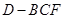 体积的最大值.
体积的最大值.