题目内容
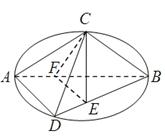
在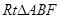 中,AB=2BF=4,C,E分别是AB,AF的中点(如下左图).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如下右图),已知D是AB的中点.
中,AB=2BF=4,C,E分别是AB,AF的中点(如下左图).将此三角形沿CE对折,使平面AEC⊥平面BCEF(如下右图),已知D是AB的中点.
(1)求证:CD∥平面AEF;
(2)求证:平面AEF⊥平面ABF;
(3)求三棱锥C-AEF的体积,
(1)详见解析;(2)详见解析;(3)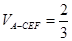 .
.
解析试题分析:(1)求证: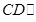 平面
平面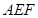 ,证明线面平行,即证线线平行,可利用三角形的中位线,或平行四边形的对边平行,本题由于
,证明线面平行,即证线线平行,可利用三角形的中位线,或平行四边形的对边平行,本题由于 是
是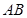 的中点,由图可知,利用中位线比较麻烦,可考虑利用平行四边形的对边平行,取
的中点,由图可知,利用中位线比较麻烦,可考虑利用平行四边形的对边平行,取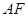 中点
中点 ,连结
,连结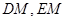 ,则
,则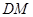 是
是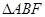 的中位线,
的中位线,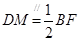 ,又
,又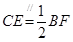 ,故,四边形
,故,四边形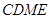 是平行四边形,从而得
是平行四边形,从而得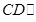 平面
平面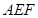 .(2)求证:平面
.(2)求证:平面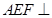 平面
平面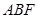 ,证明面面垂直,只需证明线面垂直,由平面图知
,证明面面垂直,只需证明线面垂直,由平面图知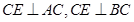 ,这样可得
,这样可得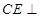 平面
平面 ,从而
,从而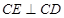 ,得
,得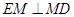 ,
,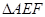 中
中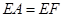 ,
, 为
为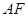 的中点,所以
的中点,所以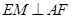 ,故
,故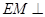 平面
平面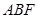 ,从而得证;(3)求三棱锥
,从而得证;(3)求三棱锥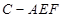 的体积,可转化为求三棱锥
的体积,可转化为求三棱锥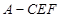 的体积.
的体积.
试题解析:(1)取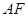 中点
中点 ,连结
,连结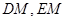 ,因为
,因为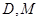 分别是
分别是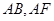 的中点,
的中点,
所以 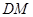 是
是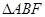 的中位线,
的中位线,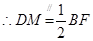 ,且
,且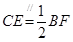 ,四边形
,四边形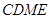 是平行四边形,所以
是平行四边形,所以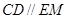 ,又
,又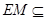 平面
平面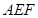 ,且
,且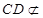 平面
平面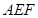 ,
,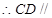 平面
平面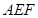 ;..........4分
;..........4分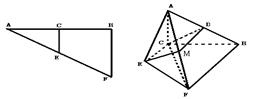
由左图知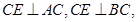 ,
,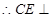 平面
平面 ,又且右图中
,又且右图中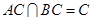
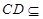 平面
平面 ,
,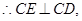 所以四边形
所以四边形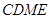 为矩形,则
为矩形,则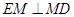 ,
,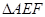 中
中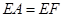 ,
, 为
为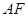 的中点,
的中点,
所以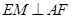 且
且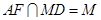 ,所以
,所以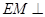 平面
平面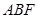 ,又
,又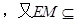 平面
平面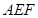 ,平面
,平面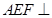 平面
平面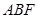
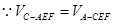 ,由左图知
,由左图知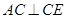 ,又面AEC⊥平面BCEF,且AEC
,又面AEC⊥平面BCEF,且AEC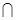 平面BCEF=CE,
平面BCEF=CE,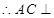 平面
平面 ,即AC为三棱锥
,即AC为三棱锥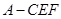 的高,
的高,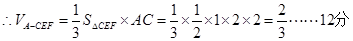
考点:线面平行,面面垂直的判断,求几何体的体积.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
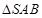 ,
,  为底面圆周上一点.
为底面圆周上一点.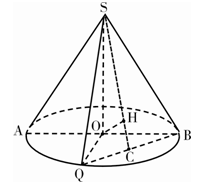
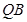 的中点为
的中点为 ,
,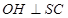 ,求证
,求证 平面
平面 ;
;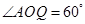 ,
,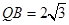 ,求此圆锥的全面积.
,求此圆锥的全面积.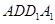 和三棱锥
和三棱锥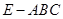 组合而成,点
组合而成,点 、
、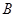 、
、 在圆
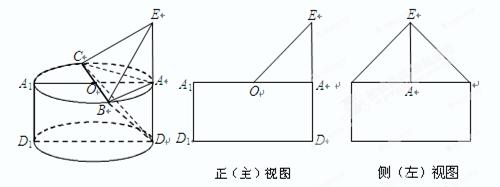
在圆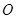 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图4所示,其中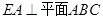 ,
,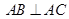 ,
,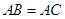 ,
,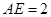 .
.
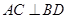 ;
;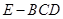 的体积.
的体积.
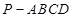 中,底面
中,底面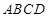 为矩形,
为矩形,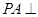 平面
平面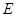 在线段
在线段 上,
上,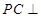 平面
平面 .
.
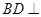 平面
平面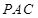 .;
.;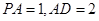 ,求三棱锥
,求三棱锥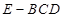 的体积.
的体积.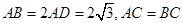 ,F是AB上的一点,且
,F是AB上的一点,且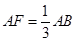 ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知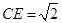
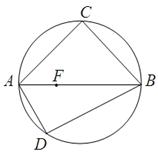
 平面BCE
平面BCE 中,底面
中,底面 是菱形,
是菱形,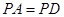 ,
,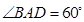 ,
,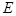 是
是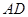 的中点,点
的中点,点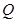 在侧棱
在侧棱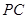 上.
上.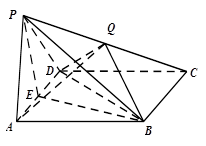
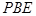 ;
; //平面
//平面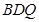 ;
;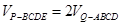 ,试求
,试求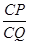 的值.
的值.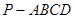 中,
中,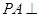 平面
平面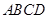 ,底面
,底面 是平行四边形,
是平行四边形,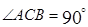 ,
,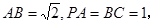
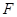 是
是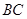 的中点
的中点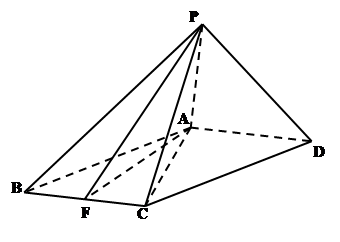
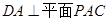
 上确定一点
上确定一点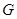 ,使
,使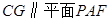 ,求三棱锥
,求三棱锥 的体积.
的体积.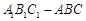 中,侧面
中,侧面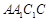
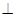 底面ABC,底面ABC是边长为2的等边三角形,侧面
底面ABC,底面ABC是边长为2的等边三角形,侧面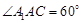 ,E、F分别是
,E、F分别是 、AB的中点.
、AB的中点.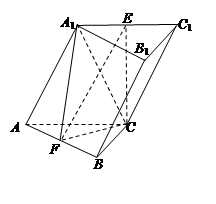
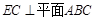 ;
; 的体积.
的体积.