题目内容
【题目】函数f(x)=(x2﹣3)ex , 当m在R上变化时,设关于x的方程f2(x)﹣mf(x)﹣ ![]() =0的不同实数解的个数为n,则n的所有可能的值为( )
=0的不同实数解的个数为n,则n的所有可能的值为( )
A.3
B.1或3
C.3或5
D.1或3或5
【答案】A
【解析】解:函数f(x)=(x2﹣3)ex的导数为f′(x)=(x+3)(x﹣1)ex , 当x>1或x<﹣3时,f′(x)>0,f(x)递增;
当﹣3<x<1时,f′(x)<0,f(x)递减.
即有f(x)在x=1处取得极小值﹣2e;在x=﹣3处取得极大值6e﹣3 ,
作出f(x)的图象,如图所示;
关于x的方程f2(x)﹣mf(x)﹣ ![]() =0,
=0,
由判别式为m2+ ![]() >0,方程有两个不等实根,
>0,方程有两个不等实根,
令t=f(x),则t2﹣mt﹣ ![]() =0,t1t2=﹣
=0,t1t2=﹣ ![]() <0,
<0,
则原方程有一正一负实根.
当t>6e﹣3 , y=t和y=f(x)有一个交点,
当0<t<6e﹣3 , y=t和y=f(x)有三个交点,
当﹣2e<t<0时,y=t和y=f(x)有两个交点,
当t<﹣2e时,y=t和y=f(x)没有交点,
则x的方程f2(x)﹣mf(x)﹣ ![]() =0的实根个数为3.
=0的实根个数为3.
故选:A.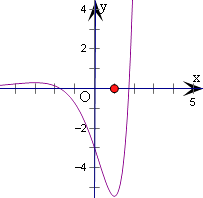

练习册系列答案
相关题目