题目内容
【题目】设函数![]() ,
, ![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() ,
, ![]() 时,求证:
时,求证: ![]() .
.
【答案】(1)增区间为: ![]() ,
, ![]() .减区间为
.减区间为![]() ,
, ![]() .(2) 见解析。
.(2) 见解析。
【解析】试题分析:(1)本问考查利用导数求函数的单调性,首先确定函数的定义域为![]() ,对
,对![]() 求导数
求导数![]() ,解
,解![]() 得增区间,解
得增区间,解![]() 得减区间;(2)本问考查利有导数证明不等式,当
得减区间;(2)本问考查利有导数证明不等式,当![]() 时,只需证:
时,只需证: ![]() ,即转化为证明
,即转化为证明![]() 当
当![]() 时成立,构造函数
时成立,构造函数![]() ,转化为证明
,转化为证明![]() 在
在![]() 时恒成立即可,转化为求函数
时恒成立即可,转化为求函数![]() 的最小值问题.
的最小值问题.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() ,当
,当![]() 时,
时, 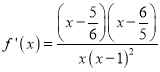 ,
,
令: ![]() ,得:
,得: ![]() 或
或![]() ,所以函数单调增区间为:
,所以函数单调增区间为: ![]() ,
, ![]() .
.
![]() ,得:
,得: ![]() ,所以函数单调减区间为
,所以函数单调减区间为![]() ,
, ![]() .
.
(2)若证![]() ,
, ![]() 成立,只需证:
成立,只需证: ![]() ,
,
即: ![]() 当
当![]() 时成立.
时成立.
设![]() .
.
∴![]() ,显然
,显然![]() 在
在![]() 内是增函数,
内是增函数,
且![]() ,
, ![]() ,
,
∴![]() 在
在![]() 内有唯一零点
内有唯一零点![]() ,使得:
,使得: ![]() ,
,
且当![]() ,
, ![]() ;
;
当![]() ,
, ![]() .
.
∴![]() 在
在![]() 递减,在
递减,在![]() 递增.
递增.
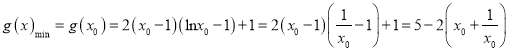 ,
,
∵![]() ,∴
,∴![]() .
.
∴![]() ,∴
,∴![]() 成立.
成立.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目