题目内容
【题目】如图2,四边形![]() 为矩形,
为矩形, ![]() ⊥平面
⊥平面![]() ,
, ![]() ,作如图3折叠,折痕
,作如图3折叠,折痕![]()
![]()
![]() ,其中点
,其中点![]() 分别在线段
分别在线段![]() 上,沿
上,沿![]() 折叠后点
折叠后点![]() 叠在线段
叠在线段![]() 上的点记为
上的点记为![]() ,并且
,并且![]() ⊥
⊥![]() .(1)证明:
.(1)证明: ![]() ⊥平面
⊥平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
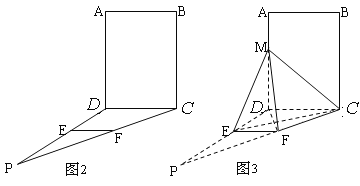
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)要证CF⊥平面MDF,只需证CF⊥MD,且CF⊥MF即可;由PD⊥平面ABCD,得出平面PCD⊥平面ABCD,即证MD⊥平面PCD,得CF⊥MD;(2)求出△CDE的面积S△CDE,对应三棱锥的高MD,计算它的体积VM-CDE.
试题解析:(1)证明:∵PD⊥平面ABCD,PD平面PCD,
∴平面PCD⊥平面ABCD;
又平面PCD∩平面ABCD=CD,MD平面ABCD,MD⊥CD,
∴MD⊥平面PCD,CF平面PCD,∴CF⊥MD;
又CF⊥MF,MD、MF平面MDF,MD∩MF=M,
∴CF⊥平面MDF;

(2)∵CF⊥平面MDF,∴CF⊥DF,
又易知∠PCD=60°,∴∠CDF=30°,∴CF=![]() CD=
CD=![]() ;
;
∵EF∥DC,∴![]() ,即
,即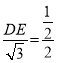 ,∴
,∴![]() ,∴
,∴![]() ,
, ![]() ,
,
![]() =
=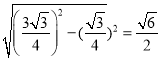 ,
,
∴![]()

练习册系列答案
相关题目