题目内容
【题目】经济学中,函数f(x)的边际函数M(x)定义为M(x)=f(x+1)﹣f(x),利润函数p(x)边际利润函数定义为M1(x)=p(x+1)﹣p(x),某公司最多生产 100 台报系统装置,生产x台的收入函数为R(x)=3000x﹣20x2(单位:元),其成本函数为C(x)=500x+4000x(单位:元),利润是收入与成本之差.
(1)求利润函数p(x)及边际利润函数M1(x);
(2)利润函数p(x)与边际利润函数M1(x)是否具有相等的最大值?
【答案】
(1)解:P(x)=R(x)﹣C(x)=3000x﹣20x2﹣(500x+4000)
=﹣20x2+2500x﹣4000(1≤x≤100,x∈N*),
M1(x)=P(x+1)﹣P(x)=2480﹣40x.(1≤x≤100,x∈N*)
(2)解:∵P(x)=﹣20 ![]() +74125,
+74125,
∴当x=62 或63 时,P(x)max=74120.
又∵M1(x) 是减函数,∴当 x=1 时,M1(x)max=2440.
故利润函数p(x)与边际利润函数M1(x)不具有相等的最大值
【解析】(1)P(x)=R(x)﹣C(x),M1(x)=P(x+1)﹣P(x).(1≤x≤100,x∈N*).(2)由P(x)=﹣20 ![]() +74125,利用二次函数的单调性可得,P(x)max . 利用一次函数的单调性可得M1(x)max .
+74125,利用二次函数的单调性可得,P(x)max . 利用一次函数的单调性可得M1(x)max .

【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查,销售单价x元和销售量y件之间的一组数据如表所示:
月份 | 7 | 8 | 9 | 10 | 11 |
销售单价x元 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y件 | 11 | 10 | 8 | 6 | 5 |
(1)根据7至11月份的数据,求出y关于x的回归直线方程;
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润? 参考公式:回归直线方程 ![]() =b
=b ![]() +a,其中b=
+a,其中b= 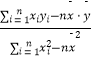 .
.
参考数据: ![]() =392,
=392, ![]() =502.5.
=502.5.