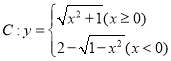题目内容
【题目】![]() ,令
,令![]()
(1)求![]() 的极值
的极值
(2)若![]() 在
在![]() 单调递增,求
单调递增,求![]() 的范围.
的范围.
【答案】(1) 当![]() 时,
时,![]() 没有极大、极小值;当
没有极大、极小值;当![]() 时,
时,![]() 的极小值为
的极小值为![]() .
.
(2) ![]()
【解析】
(1)对函数![]() 求导得到
求导得到![]() ,对
,对![]() 求导,得到
求导,得到![]() ,根据
,根据![]() 的取值范围讨论
的取值范围讨论![]() 的极值.
的极值.
(2)要求![]() 在
在![]() 单调递增,则
单调递增,则![]() ,即要使
,即要使![]() 的最小值大于等于
的最小值大于等于![]() ,根据
,根据![]() 分情况讨论,再对
分情况讨论,再对![]() 进行求导即可求最值即可求解
进行求导即可求最值即可求解
(1)![]()
![]() ,
,
![]()
![]()
![]()
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,没有极大、极小值.
上单调递增,没有极大、极小值.
②当![]() 时,令
时,令![]() ,即
,即![]() ,解得
,解得![]()

所以![]() 的极小值为
的极小值为![]()
综上所述:当![]() 时,
时, ![]() 没有极大、极小值;当
没有极大、极小值;当![]() 时,
时,![]() 的极小值为
的极小值为![]() .
.
(2)由(1)知:若![]() 在
在![]() 单调递增,则
单调递增,则![]() 在
在![]() 恒成立.
恒成立.
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
只需![]() 的最小值大于
的最小值大于![]() 即可.
即可.
![]()
![]()
②当![]() 时,
时,![]() 在
在![]() 处取得最小值,
处取得最小值,
只需有![]() 的极小值大于0.
的极小值大于0.
![]()
设![]()
![]()
![]()
![]() ,令
,令![]() =0,则
=0,则![]()
当![]() 故函数先增后减,
故函数先增后减,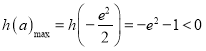 ,故
,故![]() 不成立,
不成立,
则![]() 时
时![]() 在
在![]() 单调递增不是恒成立.
单调递增不是恒成立.
综上所述: ![]() 在
在![]() 单调递增,
单调递增, ![]() 的取值范围为:
的取值范围为:![]() .
.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目