题目内容


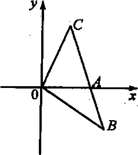
如图，在平面直角坐标系中B（4，-3），点C在第一象限内，BC交x轴于点A，∠BOC=120°，|BC|=7．
（1）求|OC|的长；
（2）记∠AOC=a，∠BOA=β．（a，β为锐角），求sina，sinβ的值．
（1）∵|OB|=5，在△OBC中，由余弦定理得：
|BC|2=|OB|2+|OC|2-2|OB|•|OC|cos120°，
即49=25+|OC|2+5|OC|，解得|OC|=3；
（2）由三角函数定义知：sinβ=-
3
5
，cosβ=
4
5
，
∵α=120°-β，∴sinα=sin（120°-β）=sin120°cosβ-cos120°sinβ=
3
2
×
4
5
+
1
2
×（-
3
5
）=
4
3
-3
10
．
练习册系列答案
相关题目
在△ABC中，已知a2+b2=c2+
2
ab，则∠C=（　　）
A．30°B．45°C．150°D．135°
在△ABC中，内角A、B、C所对边的长分别为a，b，c，且c=3，C=
π
3
，a=2b．
（1）求b边的值；（2）求△ABC的面积．
已知在△ABC中，cosA=-
4
5
，a，b，c分别是角A，B，C所对的边
（Ⅰ）若a=3
5
，c=5，求b；
（Ⅱ）若sinB=
5
13
，求cosC的值．
在△ABC中，角A，B，C的对边分别为a，b，c，且满足（2a-b）cosC=c•cosB，△ABC面积S=10
3
，c=7．
（1）求C；
（2）求a，b的值．
在△ABC中，若2cosAsinB=sinC，则△ABC的形状一定是（　　）
A．等腰三角形B．直角三角形
C．等腰直角三角形D．等边三角形
已知△ABC的周长为4(
2
+1)，且sinB+sinC=
2
sinA．
（Ⅰ）求边长a的值；
（Ⅱ）若S△ABC=3sinA，求cosA的值．
设函数f（x）=sin2x-sin（2x-
π
2
）．
（1）求函数f（x）的最大值和最小值；
（2）△ABC的内角A，B，C的对边分别为a，b，c，c=3，f（
C
2
）=
1
4
，若sinB=2sinA，求△ABC的面积．
设函数，则的值为（ ）.
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网