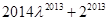题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2a-b)cosC=c•cosB,△ABC面积S=10
,c=7.
(1)求C;
(2)求a,b的值.
| 3 |
(1)求C;
(2)求a,b的值.
(1)∵(2a-b)cosC=c•cosB,
由余弦定理(2a-b)•
=c•
,即a2+b2-c2=ab,
∴cosC=
=
,
∵在三角形中,C∈(0,π),∴C=
;
(2)由S=
absinC=10
,sinC=
,得ab=40,①
由余弦定理c2=a2+b2-2abcosC得:c2=49=(a+b)2-3ab=(a+b)2-120,即a+b=13,②
联立①②解得:a=5,b=8或a=8,b=5.
由余弦定理(2a-b)•
| a2+b2-c2 |
| 2ab |
| a2+c2-b2 |
| 2ac |
∴cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
∵在三角形中,C∈(0,π),∴C=
| π |
| 3 |
(2)由S=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
由余弦定理c2=a2+b2-2abcosC得:c2=49=(a+b)2-3ab=(a+b)2-120,即a+b=13,②
联立①②解得:a=5,b=8或a=8,b=5.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
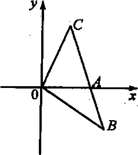
 >0,则a2014= ( )
>0,则a2014= ( )