题目内容
5.已知双曲线C:${x^2}-\frac{y^2}{2}=1$与点P(1,2).(1)求过点P(1,2)且与曲线C只有一个交点的直线方程;
(2)是否存在过点P的弦AB,使AB的中点为P,若存在,求出弦AB所在的直线方程,若不存在,请说明理由.
分析 (1)通过直线的斜率不存在和存在2中情况,存在时,将直线代入曲线C,讨论二次项系数结合根的判别式从而得到答案;
(2)假设存在,整理得到AB的斜率为$\frac{1}{2}$,从而得到直线AB的方程,进而得到结论.
解答 解:(1)当直线l的斜率不存在时,l的方程为x=1,与曲线C有一个交点.…(1分)
当直线l的斜率存在时,设直线l的方程为y-2=k(x-1),代入C的方程,
并整理得(2-k2)x2+2(k2-2k)x-k2+4k-6=0 (*)
(ⅰ)当2-k2=0,即k=±$\sqrt{2}$时,方程(*)有一个根,l与C有一个交点
所以l的方程为$\sqrt{2}x-y-\sqrt{2}+2=0或\sqrt{2}x+y-\sqrt{2}-2=0$…(3分)
(ⅱ)当2-k2≠0,即k≠±$\sqrt{2}$时
△=[2(k2-2k)]2-4(2-k2)(-k2+4k-6)=16(3-2k),
①当△=0,即3-2k=0,k=$\frac{3}{2}$时,方程(*)有一个实根,l与C有一个交点.
所以l的方程为3x-2y+1=0…(6分)
综上知:l的方程为x=1或$\sqrt{2}x-y-\sqrt{2}+2=0或\sqrt{2}x+y-\sqrt{2}-2=0$或3x-2y+1=0…(6分)
(2)假设以P为中点的弦存在,设为AB,且A(x1,y1),B(x2,y2),
则2x12-y12=2,2x22-y22=2,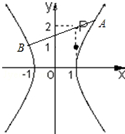
两式相减得2(x1-x2)(x1+x2)=(y1-y2)(y1+y2)…(8分)
又∵x1+x2=2,y1+y2=4,
∴2(x1-x2)=4(y1-y2)
即kAB=$\frac{{y}_{1}{-y}_{2}}{{x}_{1}{-x}_{2}}$=$\frac{1}{2}$,…(10分)
∴直线AB的方程为y-2=$\frac{1}{2}$(x-1),…(11分)
代入双曲线方程2x2-y2=2,可得,15y2-48y+34=0,
由于判别式为482-4×15×34>0,则该直线AB存在. …(12分)
点评 本题考查了直线和曲线的交点问题,考查直线方程问题,考查分类讨论思想,是一道中档题.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | |||
| Asin(ωx+φ) | 0 | 5 | -5 | 0 |
(Ⅱ)令g(x)=f (x+$\frac{π}{3}$)-1,当x∈[-$\frac{π}{6}$,$\frac{π}{3}$]时,若存在g(x)<a-2成立,求实数a的取值范围.
| A. | 3π | B. | 4π | C. | 3$\sqrt{3}$π | D. | 16π |
| A. | $y=x+\frac{4}{x}$ | B. | $y=\frac{{2({x^2}+3)}}{{\sqrt{{x^2}+2}}}$ | ||
| C. | $y=sinx+\frac{4}{sinx}(0<x<π)$ | D. | y=ex+4e-x |