题目内容
已知函数f(x)=x2-ax+3在(0,1)上为减函数,函数g(x)=x2-aln x在(1,2)上为增函数,则a的值等于( ).
| A.1 | B.2 | C.0 | D.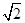 |
B
试题分析:
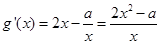 ,因为
,因为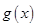 在
在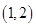 上单调递增,所以
上单调递增,所以 在
在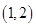 上恒成立,所以
上恒成立,所以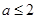 。二次函数
。二次函数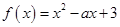 的图像是开口向上以
的图像是开口向上以 为对称轴的抛物线。因为
为对称轴的抛物线。因为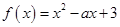 在
在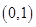 上单调递减,所以
上单调递减,所以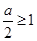 ,即
,即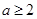 。综上可得
。综上可得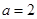 。故B正确。
。故B正确。
练习册系列答案
相关题目
题目内容
| A.1 | B.2 | C.0 | D.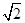 |
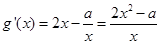 ,因为
,因为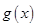 在
在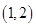 上单调递增,所以
上单调递增,所以 在
在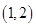 上恒成立,所以
上恒成立,所以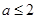 。二次函数
。二次函数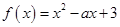 的图像是开口向上以
的图像是开口向上以 为对称轴的抛物线。因为
为对称轴的抛物线。因为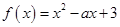 在
在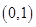 上单调递减,所以
上单调递减,所以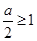 ,即
,即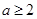 。综上可得
。综上可得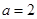 。故B正确。
。故B正确。