题目内容
已知函数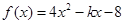
(1)若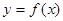 在[-3,2]上具有单调性,求实数
在[-3,2]上具有单调性,求实数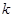 的取值范围。
的取值范围。
(2)若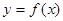 的
的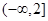 有最小值为-12,求实数
有最小值为-12,求实数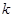 的值;
的值;
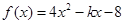
(1)若
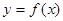 在[-3,2]上具有单调性,求实数
在[-3,2]上具有单调性,求实数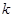 的取值范围。
的取值范围。(2)若
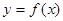 的
的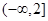 有最小值为-12,求实数
有最小值为-12,求实数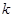 的值;
的值;(1)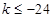 或
或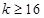 ;(2)
;(2) 或
或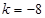
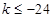 或
或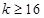 ;(2)
;(2) 或
或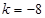
试题分析:(1)二次函数的单调性与对称轴有关,单调区间在对称轴的一侧,可数形结合解题;
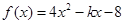 图像开口上, 对称轴为
图像开口上, 对称轴为 ,区间
,区间 在对称轴左侧
在对称轴左侧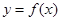 为单调减函数, 区间
为单调减函数, 区间 在对称轴右侧
在对称轴右侧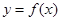 为单调增函数,
为单调增函数,(2)二次函数在区间上的最值在端点处或顶点处,遇到对称轴或区间含有待定的字母,则要按对称轴在不在区间内以及区间中点进行讨论.
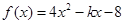 图像开口上,当对称轴为
图像开口上,当对称轴为 在区间
在区间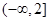 内时,最小值位于对称轴处; 当区间
内时,最小值位于对称轴处; 当区间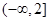 在对称轴左侧
在对称轴左侧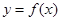 为单调减函数,最小值位于右端点处.
为单调减函数,最小值位于右端点处.试题解析:
(1)
 的对称轴为
的对称轴为
又
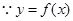 在
在 上具有单调性
上具有单调性所以
 或
或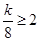
即
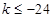 或
或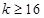
(2) 由
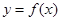 在
在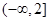 有最小值为
有最小值为
Ⅰ.当
 即
即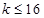 时
时
解得:
 或
或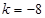
Ⅱ.当
 即
即 时
时
解得:
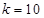 (舍)
(舍)综上所述:
 或
或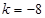

练习册系列答案
相关题目
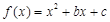 ,其中
,其中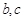 为常数.
为常数. 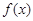 在区间
在区间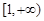 上单调,求
上单调,求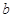 的取值范围;
的取值范围;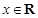 ,都有
,都有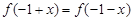 成立,且函数
成立,且函数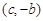 ,
,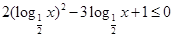 的解集为M,求当x∈M时函数
的解集为M,求当x∈M时函数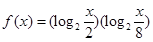 的最大、最小值.
的最大、最小值. (a>0,a≠1)
(a>0,a≠1) 满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围. ,满足
,满足 ,且
,且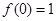 ,若在区间
,若在区间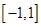 上,不等式
上,不等式 恒成立,则实数m的取值范围为 .
恒成立,则实数m的取值范围为 .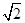
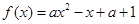 在
在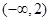 上单调递减,则
上单调递减,则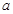 的取值范围是
的取值范围是



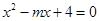 在
在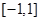 有解,则实数m的取值范围是__________.
有解,则实数m的取值范围是__________. 则
则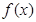 与
与 的大小关系是( )
的大小关系是( )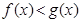

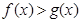
 的值的变化而变化
的值的变化而变化