题目内容
2.已知椭圆C的焦点为F1(-$\sqrt{2}$,0),F2($\sqrt{2}$,0),且椭圆C的下顶点到直线x+y-2=0的距离为3$\sqrt{2}$/2.(1)求椭圆C的方程;
(2)若一直线l:y=kx+m与椭圆C相交于A、B(A、B不是椭圆C 的顶点)两点,以AB为直径的圆过椭圆C 的上顶点,求证:直线l过定点,并求出该定点的坐标.
分析 (1)通过题意可设椭圆C的方程:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),利用点(0,-b)到直线x+y-2=0的距离公式可得b=1,结合c=$\sqrt{2}$,计算即得结论;
(2)通过联立直线l:y=kx+m与椭圆C的方程,利用韦达定理,结合AQ⊥BQ,计算可得m=1或m=-$\frac{1}{2}$,进而可得结论.
解答 (1)解:∵椭圆C的焦点为F1(-$\sqrt{2}$,0),F2($\sqrt{2}$,0),
∴可设椭圆C的方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
∵椭圆C的下顶点(0,-b)到直线x+y-2=0的距离为$\frac{3\sqrt{2}}{2}$,
∴$\frac{|-b-2|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$,解得b=1,
∴a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{(\sqrt{2})^{2}+{1}^{2}}$=$\sqrt{3}$,
∴椭圆C的方程为:$\frac{{x}^{2}}{3}+{y}^{2}=1$;
(2)证明:设椭圆C的上顶点为Q(0,1),
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$,消去y整理得:($\frac{1}{3}$+k2)x2+2kmx+m2-1=0,
∵直线l:y=kx+m与椭圆C相交于A、B(A、B不是椭圆C的顶点)两点,
∴△=4k2m2-4($\frac{1}{3}$+k2)(m2-1)=4(k2-$\frac{1}{3}$m2+$\frac{1}{3}$)>0,即3k2-m2+1>0,
设A(x1,y1),B(x2,y2),
则x1+x2=-$\frac{6km}{1+3{k}^{2}}$,x1x2=$\frac{3({m}^{2}-1)}{1+3{k}^{2}}$,
∴y1+y2=k(x1+x2)+2m=$\frac{2m}{1+3{k}^{2}}$,
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=k2•$\frac{3({m}^{2}-1)}{1+3{k}^{2}}$+km(-$\frac{6km}{1+3{k}^{2}}$)+m2=$\frac{{m}^{2}-3{k}^{2}}{1+3{k}^{2}}$,
∵AQ⊥BQ,∴x1x2+(y1-1)(y2-1)=0,即x1x2+y1y2-(y1+y2)+1=0,
∴$\frac{3({m}^{2}-1)}{1+3{k}^{2}}$+$\frac{{m}^{2}-3{k}^{2}}{1+3{k}^{2}}$-$\frac{2m}{1+3{k}^{2}}$+1=0,
化简得:2m2-m-1=0,解得m=1或m=-$\frac{1}{2}$,
当m=1时,直线l:y=kx+1过定点Q(0,1),与已知矛盾;
当m=-$\frac{1}{2}$时,满足3k2-m2+1>0,
此时直线l:y=kx-$\frac{1}{2}$过定点(0,-$\frac{1}{2}$),
∴直线l过定点(0,-$\frac{1}{2}$).
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | [1,2] | B. | (1,2] | C. | (1,+∞) | D. | [2,+∞) |
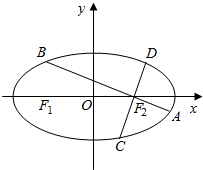 如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.
如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.