题目内容
16.设实数x1,x2,…,xn中的最大数为max{x1,x2,…,xn},最小数为min{x1,x2,…,xn}.已知1≤x≤y且三数1,x,y能构成三角形的三边长,记t=max{$\frac{1}{x}$,$\frac{x}{y}$,y}•min{$\frac{1}{x}$,$\frac{x}{y}$,y},求:(1)若y=x2,则t的最小值为1;
(2)t的取值范围是$[1,\frac{{1+\sqrt{5}}}{2})$.
分析 (1)若y=x2,则由1≤x≤y可得$\frac{1}{x}$=$\frac{x}{y}$≤y,此时此时t=x,当且仅当x=y=1时,t的最小值为1;
(2)显然max{$\frac{1}{x}$,$\frac{x}{y}$,y}=y,又min{$\frac{1}{x}$,$\frac{x}{y}$,y}=$\left\{\begin{array}{l}\frac{1}{x},y<{x}^{2}\\ \frac{x}{y},y≥{x}^{2}\end{array}\right.$,分类讨论,作出可行区域,求出在第一象限内的交点坐标,即可求出t的取值范围.
解答 解:(1)y=x2,由1≤x≤y,
可得$\frac{1}{x}$=$\frac{x}{y}$≤y,
此时t=max{$\frac{1}{x}$,$\frac{x}{y}$,y}•min{$\frac{1}{x}$,$\frac{x}{y}$,y}=$\frac{x}{y}$•y=x,
当且仅当x=y=1时,t的最小值为1,
(2)∵1≤x≤y且三数1,x,y能构成三角形的三边长,
∴max{$\frac{1}{x}$,$\frac{x}{y}$,y}=y,又min{$\frac{1}{x}$,$\frac{x}{y}$,y}=$\left\{\begin{array}{l}\frac{1}{x},y<{x}^{2}\\ \frac{x}{y},y≥{x}^{2}\end{array}\right.$,
①当y<x2时,t=$\frac{y}{x}$,作出可行区域$\left\{\begin{array}{l}1≤x≤y\\ y<x+1\\ y<{x}^{2}\end{array}\right.$,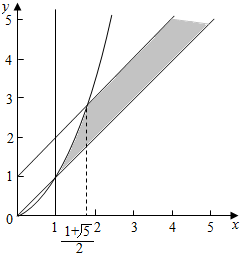
因抛物线y=x2与直线y=x及y=x+1在第一象限内的交点分别是(1,1)和($\frac{1+\sqrt{5}}{2}$,$\frac{3+\sqrt{5}}{2}$),从而1<t<$\frac{1+\sqrt{5}}{2}$
②当y≥x2时,t=x,作出可行区域$\left\{\begin{array}{l}1≤x≤y\\ y<x+1\\ y≥{x}^{2}\end{array}\right.$,
因抛物线y=x2与直线y=x及y=x+1在第一象限内的交点分别是(1,1)和($\frac{1+\sqrt{5}}{2}$,$\frac{3+\sqrt{5}}{2}$),从而1≤t<$\frac{1+\sqrt{5}}{2}$
综上所述,t的取值范围是[1,$\frac{1+\sqrt{5}}{2}$).
故答案为:[1,$\frac{1+\sqrt{5}}{2}$).
故答案为:1,[1,$\frac{1+\sqrt{5}}{2}$)
点评 本题考查t的取值范围,考查抛物线知识,考查新定义,确定可行区域,求出在第一象限内的交点坐标是关键.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
| A. | 有最大值0 | B. | 最大值2 | C. | 最小值0 | D. | 最小值-6 |
 如图,在矩形ABCD中,AB=2,AD=1,O为AB中点,抛物线的一部分在矩形内,点O为抛物线顶点,点C,D在抛物线上,在矩形内随机地投放一点,则此点落在阴影部分的概率为$\frac{1}{3}$.
如图,在矩形ABCD中,AB=2,AD=1,O为AB中点,抛物线的一部分在矩形内,点O为抛物线顶点,点C,D在抛物线上,在矩形内随机地投放一点,则此点落在阴影部分的概率为$\frac{1}{3}$.