题目内容
12.设f(x)是定义在R上的偶函数,且f(2+x)=f(2-x),当x∈[-2,0]时,f(x)=($\frac{\sqrt{2}}{2}$)x-1,若在区间(-2,6)内关于x的方程f(x)-loga(x+2)=0(a>0),有4个不同的根,则a的范围是(8,+∞).分析 由已知中可以得到函数f(x)是一个周期函数,且周期为4,将方程f(x)-loga(x+2)=0恰有4个不同的实数解,转化为函数f(x)的与函数y=-loga(x+2)的图象恰有4个不同的交点,数形结合即可得到实数a的取值范围.
解答 解:∵对于任意的x∈R,都有f(x-2)=f(2+x),
∴f(x+4)=f[2+(x+2)]=f[(x+2)-2]=f(x),
∴函数f(x)是一个周期函数,且T=4.
又∵当x∈[-2,0]时,f(x)=($\frac{\sqrt{2}}{2}$)x-1,且函数f(x)是定义在R上的偶函数,
若在区间(-2,6)内关于x的方程f(x)-loga(x+2)=0恰有4个不同的实数解,
则函数y=f(x)与y=loga(x+2)在区间(-2,6)上有四个不同的交点,如下图所示: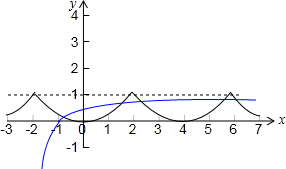
又f(-2)=f(2)=f(6)=1,
则对于函数y=loga(x+2),
由题意可得,当x=6时的函数值小于1,
即loga8<1,
由此解得:a>8,
∴a的范围是(8,+∞)
故答案为:(8,+∞).
点评 本题考查的知识点是根的存在性及根的个数判断,指数函数与对数函数的图象与性质,其中根据方程的解与函数的零点之间的关系,将方程根的问题转化为函数零点问题,是解答本题的关键,体现了转化和数形结合的数学思想,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
3.若关于x的方程$\sqrt{1-{x}^{2}}$=lg(x-a)有正数解,则实数a的取值范围( )
| A. | -10<a≤0 | B. | -1<a≤0 | C. | 0≤a<1 | D. | 0≤a<10 |
17.执行如图所示的程序框图,若输出的结果是$\frac{12}{13}$,则循环体的判断框内①处应填( )
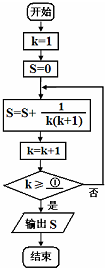

| A. | 11? | B. | 12? | C. | 13? | D. | 14? |
4.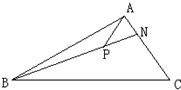 如右图,在△ABC中,$\overrightarrow{AN}$=$\frac{1}{4}$$\overrightarrow{NC}$,P是BN上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,则实数m的值为( )
如右图,在△ABC中,$\overrightarrow{AN}$=$\frac{1}{4}$$\overrightarrow{NC}$,P是BN上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,则实数m的值为( )
 如右图,在△ABC中,$\overrightarrow{AN}$=$\frac{1}{4}$$\overrightarrow{NC}$,P是BN上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,则实数m的值为( )
如右图,在△ABC中,$\overrightarrow{AN}$=$\frac{1}{4}$$\overrightarrow{NC}$,P是BN上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+$\frac{1}{6}$$\overrightarrow{AC}$,则实数m的值为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 3 |
1.双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,若F关于直线y=$\sqrt{3}$x的对称点P在双曲线上,则C的离心率为( )
| A. | 2 | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{3}$+1 |