题目内容
【题目】某运输公司接受了向抗洪救灾地区每天送至少![]() 支援物资的任务.该公司有
支援物资的任务.该公司有![]() 辆载重
辆载重![]() 的
的![]() 型卡车与
型卡车与![]() 辆载重为
辆载重为![]() 的
的![]() 型卡车,有
型卡车,有![]() 名驾驶员,每辆卡车每天往返的次数为
名驾驶员,每辆卡车每天往返的次数为![]() 型卡车
型卡车![]() 次,
次,![]() 型卡车
型卡车![]() 次;每辆卡车每天往返的成本费
次;每辆卡车每天往返的成本费![]() 型为
型为![]() 元,
元,![]() 型为
型为![]() 元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排
元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排![]() 型或
型或![]() 型卡车,所花的成本费分别是多少?
型卡车,所花的成本费分别是多少?
【答案】只用![]() 型车,所花的成本费最低为
型车,所花的成本费最低为![]() (元),只用
(元),只用![]() 型车,成本费为
型车,成本费为![]() (元).
(元).
【解析】
主要考查二元一次不等式(组)的几何意义,运用所学知识,求解最值问题。
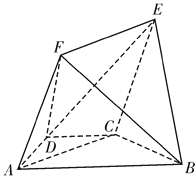
解:设需![]() 型、
型、![]() 型卡车分别为
型卡车分别为![]() 辆和
辆和![]() 辆.列表分析数据.
辆.列表分析数据.
|
| 限量 | |
车辆数 |
|
|
|
运物吨数 |
|
|
|
费用 |
|
|
|
由表可知![]() ,
,![]() 满足的线性条件:
满足的线性条件:
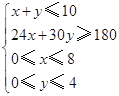 ,且
,且![]() .
.
作出线性区域,如图所示,
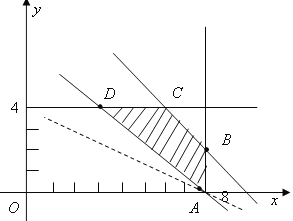
可知当直线![]() 过
过![]() 时,
时,![]() 最小,但
最小,但![]() 不是整点,继续向上平移直线
不是整点,继续向上平移直线![]() 可知,
可知,![]() 是最优解.这时
是最优解.这时![]() (元),即用8辆
(元),即用8辆![]() 型车,0辆
型车,0辆![]() 型车,成本费最低.
型车,成本费最低.
若只用![]() 型车,成本费为
型车,成本费为![]() (元),只用
(元),只用![]() 型车,成本费为
型车,成本费为![]() (元).
(元).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】近期,某公交公司与银行开展云闪付乘车支付活动,吸引了众多乘客使用这种支付方式.某线路公交车准备用20天时间开展推广活动,他们组织有关工作人员,对活动的前七天使用云闪付支付的人次数据做了初步处理,设第x天使用云闪付支付的人次为y,得到如图所示的散点图.
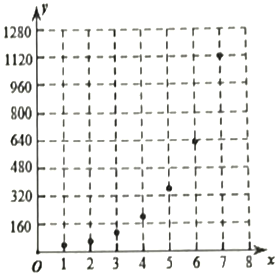
由统计图表可知,可用函数y=abx拟合y与x的关系
(1)求y关于x的回归方程;
(2)预测推广期内第几天起使用云闪付支付的人次将超过10000人次.
附:①参考数据
|
|
|
|
|
|
4 | 360 | 2.30 | 140 | 14710 | 71.40 |
表中vi=lgyi,![]() lgyi
lgyi
②参考公式:对于一组数据(u1,v1),(u2,v2)…,(un,vn),其回归直线v=α+βu的斜率和截距的最小二乘估计分别为β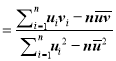 ,α
,α![]() .
.