题目内容
【题目】已知椭圆 ![]() 的焦距为
的焦距为![]() ,斜率为
,斜率为![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,若线段
两点,若线段![]() 的中点为
的中点为![]() ,且直线
,且直线![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过左焦点![]() 斜率为
斜率为![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]()
![]() 为椭圆上一点,且满足
为椭圆上一点,且满足![]() ,问:
,问:![]() 是否为定值?若是,求出此定值,若不是,说明理由.
是否为定值?若是,求出此定值,若不是,说明理由.
【答案】(1) ![]() .
.
(2) ![]() 为定值
为定值![]() .过程见解析.
.过程见解析.
【解析】分析:(1)焦距说明![]() ,用点差法可得
,用点差法可得![]() =
=![]() .这样可解得
.这样可解得![]() ,得椭圆方程;
,得椭圆方程;
(2)若![]() ,这种特殊情形可直接求得
,这种特殊情形可直接求得![]() ,在
,在![]() 时,直线
时,直线![]() 方程为
方程为![]() ,设
,设![]() ,把直线方程代入椭圆方程,后可得
,把直线方程代入椭圆方程,后可得![]() ,然后由纺长公式计算出弦长
,然后由纺长公式计算出弦长![]() ,同时直线
,同时直线![]() 方程为
方程为![]() ,代入椭圆方程可得
,代入椭圆方程可得![]() 点坐标,从而计算出
点坐标,从而计算出![]() ,最后计算
,最后计算![]() 即可.
即可.
详解:(1)由题意可知![]() ,设
,设![]() ,代入椭圆可得:
,代入椭圆可得:
![]() ,两式相减并整理可得,
,两式相减并整理可得,
![]() ,即
,即![]() .
.
又因为![]() ,
,![]() ,代入上式可得,
,代入上式可得,![]() .
.
又![]() ,所以
,所以![]() ,
,
故椭圆的方程为![]() .
.
(2)由题意可知,![]() ,当
,当![]() 为长轴时,
为长轴时,![]() 为短半轴,此时
为短半轴,此时
![]() ;
;
否则,可设直线![]() 的方程为
的方程为![]() ,联立
,联立 ,消
,消![]() 可得,
可得,
![]() ,
,
则有:![]() ,
,
所以![]()
设直线![]() 方程为
方程为![]() ,联立
,联立 ,根据对称性,
,根据对称性,
不妨得![]() ,
,
所以![]() .
.
故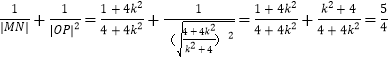 ,
,
综上所述,![]() 为定值
为定值![]() .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】某地西红柿从2月1号起开始上市,通过市场调查,得到西红柿种植成本![]() (单位:元/100
(单位:元/100![]() )与上市时间
)与上市时间![]() (距2月1日的天数,单位:天)的数据如下表:
(距2月1日的天数,单位:天)的数据如下表:
时间 | 50 | 110 | 250 |
成本 | 150 | 108 | 150 |
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本![]() 与上市时间
与上市时间![]() 的变化关系:
的变化关系:![]() ;
;
(2)利用(1)中选取的函数,求西红柿种植成本![]() 最低时的上市天数
最低时的上市天数![]() 及最低种植成本.
及最低种植成本.
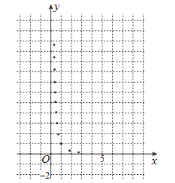
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.