题目内容
Δ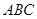 两个顶点
两个顶点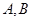 的坐标分别是
的坐标分别是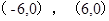 ,边
,边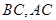 所在直线的斜率之积等于
所在直线的斜率之积等于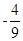 ,求顶点
,求顶点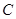 的轨迹方程,并画出草图。
的轨迹方程,并画出草图。
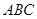 两个顶点
两个顶点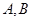 的坐标分别是
的坐标分别是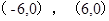 ,边
,边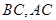 所在直线的斜率之积等于
所在直线的斜率之积等于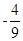 ,求顶点
,求顶点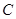 的轨迹方程,并画出草图。
的轨迹方程,并画出草图。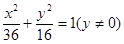
试题分析:设
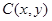
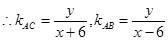
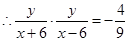
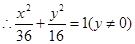
点评:求轨迹方程的题目大体分为以下几步:建系设点,寻找动点满足的关系,将关系坐标化,整理化简,除去多余点

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
题目内容
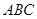 两个顶点
两个顶点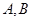 的坐标分别是
的坐标分别是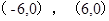 ,边
,边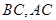 所在直线的斜率之积等于
所在直线的斜率之积等于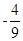 ,求顶点
,求顶点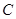 的轨迹方程,并画出草图。
的轨迹方程,并画出草图。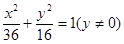
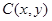
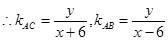
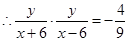
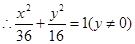

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案